Testmengen in der ganzzahligen Optimierung

Die Kenntnis von Testmengen ermöglicht, ganzzahlige Optimierungsprobleme mittels eines primalen Optimierungsalgorithmus zu lösen. Testmengen sind durch folgende Eigenschaft charakterisiert: Eine zulässige Lösung x eines ganzzahligen Optimierungsproblems ist entweder optimal, oder es gibt ein Element t der Testmenge, so daß die Differenz x-t wieder zulässig ist und bezüglich der Zielfunktion einen besseren Wert hat. Ist also eine zulässige Lösung gegeben, kann man iterativ durch Subtraktion von Testmengenelementen zur Optimallösung gelangen.

  

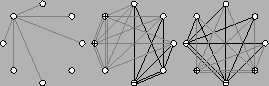
Abbildung: Repräsentanten der drei Klassen von Elementen in der minimalen Testmenge für K₈

Conti und Traverso haben einen interessanten Zusammenhang zwischen ganzzahliger Optimierung und Gröbnerbasen in der kommutativen Algebra aufgezeigt. Dabei werden die Differenzen von zulässigen Lösungen zu einer ganzen Familie von geeigneten ganzzahligen Programmen in Beziehung zu einem Binomideal in einem Polynomring gesetzt. Bei geeigneter Wahl einer Monomordnung entspricht dann die reduzierte Gröbner-Basis dieses Ideals der minimalen Testmenge für die Problemfamilie. Theoretisch ergibt sich dadurch die Möglichkeit, mit Hilfe algebraischer Methoden ganzzahlige Optimierungsprobleme zu lösen: Erst wird mit dem Buchberger-Algorithmus die Testmenge ermittelt. Anschließend wird ausgehend von einer zulässigen Lösung eine Folge von Verbesserungsschritten ,,entlang`` Elementen der Testmenge ausgeführt, bis das Optimum erreicht ist. Obwohl in dem betrachteten Fall die Gröbnerbasis nur zu Idealen mit recht spezieller Struktur berechnet werden muß, ist dieser Ansatz aufgrund der hohen Laufzeit des Buchberger Algorithmus und der potentiell gewaltigen Größe der Basis für Beispiele mit vielen Variablen sehr problematisch. Daher werden die algebraischen Methoden nicht als direkte Lösungsverfahren betrachtet. Statt dessen werden die Methoden der Computeralgebra im hier verfolgten Ansatz dazu eingesetzt, die minimalen Testmengen zu ganzzahligen Optimierungsproblemen zu berechnen, um anschließend aus den so gewonnenen Informationen Aussagen über die Struktur der Testmengen zu ermöglichen. So ist es beispielsweise im Falle der Bestimmung einer Knotenüberdeckung minimalen Gewichts in einem Graphen gelungen, die Struktur der Testmenge vollständig zu beschreiben, und zwar unabhängig von der Tatsache, daß zu ihrer Berechnung aufwendige algebraische Methoden eingesetzt wurden. Für den Spezialfall einer minimalen Knotenüberdeckung in einem vollständigen Graphen gilt der Satz:

Bis auf ein Element ist die reduzierte Gröbnerbasis genau die Menge aller Vektoren, die entweder negativ bzgl. der Monomordnung sind und das Gewicht um 1 erniedrigen, oder das Gewicht unverändert lassen und positiv bzgl. der Ordnung sind. In Abbildung 1.8 sind typische Repräsentanten der minimalen Testmenge für den K₈ graphisch dargestellt. Das linke Element und Elemente vom mittleren Typ erniedrigen das Gewicht einer Knotenüberdeckung, während die Elemente vom rechten Typ lediglich für eine Umverteilung der Gewichte stehen. Im Falle beliebiger Graphen kommt noch eine dritte Klasse von Elementen zur Testmenge hinzu, die die komplizierteren Adjazenz-Beziehungen zwischen Knoten mit veränderten Gewichten widerspiegelt. Ziel ist es, auch bei schweren ganzzahligen Optimierungsproblemen eine - möglicherweise unvollständige - Beschreibung der Struktur der Testmenge ermitteln zu können. Diese Kenntnisse können dann in einer Verbesserungsheuristik genutzt werden.