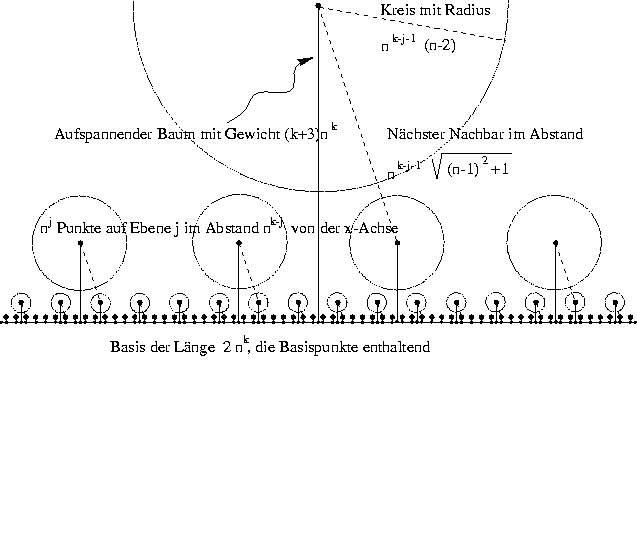
Abbildung: Eine Familie von Punktmengen mit großer Tourlänge
In den Bereichen Netzwerkdesign und VLSI steht man häufig vor der Aufgabe, ein System von Verbindungen mit möglichst günstigen Gesamtkosten zu erstellen; aus Stabilitäts- und Kapazitätsgründen existieren dabei aber Obergrenzen für die Belastung der einzelnen Knoten.
Mathematisch gesprochen steht man vor folgendem Problem:
Gegeben ein Graph G mit Kosten w(e) für jede
Kante e sowie einer Kapazitätsschranke d(v) für
jeden Knoten v. Gesucht ist ein zusammenhängender
Teilgraph mit kleinstmöglichen Gesamtkosten, in dem
kein Knoten höheren Grad als d(v) hat.
Da sich das bekannte Traveling-Salesman-Problem
als eine solche Fragestellung formulieren läßt,
ist nicht damit zu rechnen, daß es einen
exakten Algorithmus gibt, der für jede
Probleminstanz in polynomialer Laufzeit
eine optimale Lösung findet. Aus diesem
Grunde ist man daran interessiert,
Methoden zu entwickeln, die in kurzer Zeit möglichst
gute Approximationen von Optimallösungen
liefern. Ein Ansatz dafür besteht darin, von
einem zusammenhängenden Netzwerk kleinstmöglichen
Gesamtgewichts auszugehen und diesen minimalen
aufspannenden Baum T dann so zu modifizieren, daß
die Gradbeschränkungen der einzelnen Knoten
eingehalten werden. Es gelang uns, mit diesen
Ansatz eine Netzwerkflußmethode zu entwickeln,
die in verschiedener Hinsicht optimal ist:
Unser Algorithmus kann im allgemeinen von keiner
Methode unterboten werden, die nur Informationen
über Topologie und Kantengewichte
eines minimalen aufspannenden Baumes sowie die
Dreiecksungleichung benutzt. Wir können garantieren,
daß die Kosten des konstruierten Baumes
diejenigen des minimalen aufspannenden Baumes T
um nicht mehr als einen Faktor von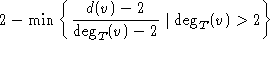 
übersteigt, vorausgesetzt, daß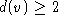 
für
alle Knoten v gilt. (Dabei ist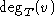 
der Grad von
v im minimalen aufspannenden Baum T.) Dies ist der
bestmögliche derartige Faktor. Und schließlich hat eine
Variante unserer Methode lineare, also optimale
Laufzeit und garantiert gleichzeitig diesen
Approximationsfaktor.
Aus unseren Ergebnissen lassen sich zudem Aussagen
über Spezialfälle des Problemes ableiten, in denen
die Kostenfunktion durch geometrische Abstände
der Netzknoten gegeben ist. Insbesondere für den
Fall von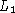 
-Abständen in der Ebene (die sogenannte Manhattan-Metrik,
die vor allem für VLSI-Probleme von entscheidender Bedeutung
ist) folgt, daß der obengenannte Quotient den Wert
von 1,5 nicht übersteigen kann, wenn die Gradbeschränkungen
der Knoten d(v)=3 betragen. Dies ist zur Zeit der beste bekannte
Wert. An dieser Stelle gibt es noch eine Reihe von
offenen Fragen, da nicht klar ist, ob für d(v)=3 tatsächlich größere
Quotienten als 
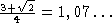auftreten
können. Es gelang uns
aber, den seit einiger Zeit offenen Fall von d(v)=2 zu lösen,
indem wir eine Klasse von geometrischen Beispielen
konstruierten, für die der genannte Quotient beliebig nahe an 2
kommen kann.