

Eine der wichtigsten Methoden der Optimierung für die Anwendung ist die Lineare Optimierung, bei der eine lineare Zielfunktion unter einer Reihe von linearen Nebenbedingungen maximiert wird. Die folgenden beiden Abschnitte behandeln Fragestellungen, die aus der Linearen Programmierung motiviert sind.
In den letzten Jahren haben J. Nešetřil und Koautoren Dualität als alternative Existenz gewisser Homomorphismen studiert. Zwei der Ausgangspunkte waren Graphen und Digraphen mit ihren Homomorphismen. Für Graphen zum Beispiel ist die Homomorphismen-Dualität eindeutig - und trivial:

Ein Kenner von Graphenhomomorphismen erkennt sofort die tiefe Weisheit, die in dieser Aussage steckt: Entweder ein Graph hat eine Kante, oder er hat keine. Bei Digraphen ist die Situation diffiziler. Hier definiert jeder gerichtete Baum eine Dualität.
Da in der kombinatorischen Optimierung die Dualität der linearen Programmierung in gewissem Sinne eine Art gemeinsamen Nenner fast aller bekannten Dualitätssätze bildet, haben wir die Fragestellung untersucht, inwiefern diese Dualität als Homomorphismendualität aufgefaßt werden kann, und wenn, ob sie dann eindeutig ist.
Die Dualitätstheorie der Linearen Programmierung führt auf kanonische Weise zu einem Axiomensystem für orientierte Matroide. Ausgehend von einem Vorschlag von Lovász und Schrijver haben wir daher untersucht, inwiefern sich dieser allgemeine Dualitätsbegriff in den Rahmen der Homomorphismendualität integrieren läßt. Der offensichtliche Kandidat für die Morphismen sind ,,strong maps``, die das kombinatorische Gegenstück zu linearen Abbildungen sind. Um zu einem sinnvollen Ansatz zu kommen, muß man zunächst eine affine Version dieser Abbildungen definieren. Allerdings ist hier die einzige existierende Homomorphismendualität wieder nur eine triviale Aussage: Entweder ein Vektorraum hat in der ersten Koordinate irgendwo einen Nicht-Nulleintrag, oder eben nicht. Dies liegt daran, daß die ,, strong maps`` zwar das Zusammenfassen identischer Koordinaten zulassen aber keine Koordinatenverdopplung, obwohl es sich im linearen Fall hierbei um einen Isomorphismus handelt. Trägt man dieser Tatsache Rechnung und erweitert den Morphismenbegriff, so erhält man als Resultat:

Polarität, oder Ordnungsdualität von Polyedern, ist eine andere Form der Dualität als die der Linearen Programmierung. Die Unterschiede und Zusammenhänge sind noch nicht völlig verstanden.
Was die Unterschiede angeht, so konnten wir einen Beitrag leisten, der sich harmonisch in klassische Resultate aus der projektiven Geometrie einreiht.
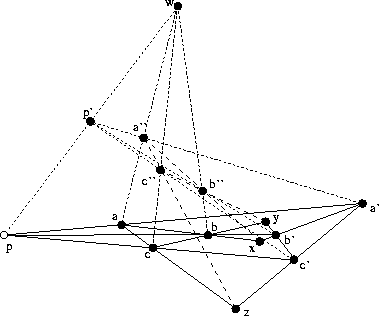
Abbildung: Diese Koerweiterung des Non-Desargues-Matroids hat keinen Adjoint eines Adjoints
Ein nichtlineares Matroid M vom Rang mindestens 4 kann niemals iterierte
Polare beliebigen Grades haben, da diese gegen einen projektiven Raum
,,konvergieren`` würden, in den M eingebettet ist.
Allerdings war bislang kein Beispiel eines orientierten Matroids mit
Polarer bekannt, dessen Polare sich nicht polarisieren läßt.
Es gelang uns, hierfür ein Beispiel zu konstruieren -
siehe Abbildung  .
Die nicht orientierte Version dieses Beispiels ist eine Koerweiterung
des Non-Desargues-Matroids mit einem koparallelen Element. Im
orientierten Fall nennt man diese Erweiterung ,,Lawrence-Konstruktion``.
Die Nähe eines solchen Beispiels zum Desarguesschen Satz war
eigentlich zu erwarten, da gilt:
.
Die nicht orientierte Version dieses Beispiels ist eine Koerweiterung
des Non-Desargues-Matroids mit einem koparallelen Element. Im
orientierten Fall nennt man diese Erweiterung ,,Lawrence-Konstruktion``.
Die Nähe eines solchen Beispiels zum Desarguesschen Satz war
eigentlich zu erwarten, da gilt:
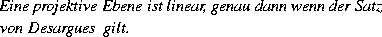
Die Existenz einer orientierten Polaren zeigen wir mittels eines neuen Konstruktionsverfahrens, das unter gewissen Voraussetzungen Elemente außerhalb einer Hyperebene verdoppelt.