Schranken

Für einen erfolgreichen Branch-&-Bound-Algorithmus sind gute Schranken, die sich leicht berechnen lassen, von besonderer Bedeutung. Sie erlauben es, die Baumsuche effizient durchzuführen, da sich große Teile des Suchbaumes schnell als irrelevant für die Suche nach einem Optimum identifizieren lassen. Neben einfachen Schranken für den eindimensionalen Fall gab es bislang eine Reihe von ,,handgestrickten`` Varianten für zwei- oder dreidimensionale Probleme. Die Gültigkeit dieser Schranken mußte bislang aber jeweils einzeln und relativ mühsam bewiesen werden.

Durch Untersuchungen am klassischen eindimensionalen Bin-Packing-Problem gelangten wir zu einem neuen allgemeinen Ansatz, mit dem sich die Entwicklung unterer Schranken systematisieren und vereinfachen läßt. Gleichzeitig erhielten wir mit unserer Methode der sogenannten ,,dualzulässigen Funktionen`` eine Reihe von verallgemeinerten Schranken, die sowohl theoretisch wie praktisch eine Reihe von nützlichen Eigenschaften aufweisen:

 

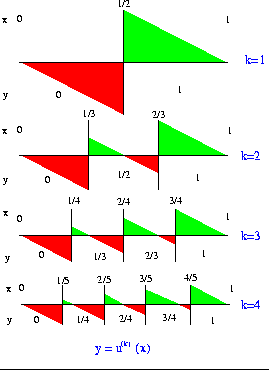
Abbildung: Die Volumenbilanz für eine Familie dualzulässiger Funktionen

Sie sind extrem schnell und einfach zu berechnen, sie liefern das Optimum für ganze Klassen von Probleminstanzen, für die andere Typen von Schranken besonders schlecht abschneiden, sie besitzen auch im schlechtesten Falle eine hervorragende Gütegarantie und schließlich schneiden sie auch in etablierten Praxistests deutlich besser ab als bisher gebräuchliche einfache Schranken.