Abbildung: Ein kompliziertes Softwarepaket: Struktur und Sichtbarkeitsdarstellung
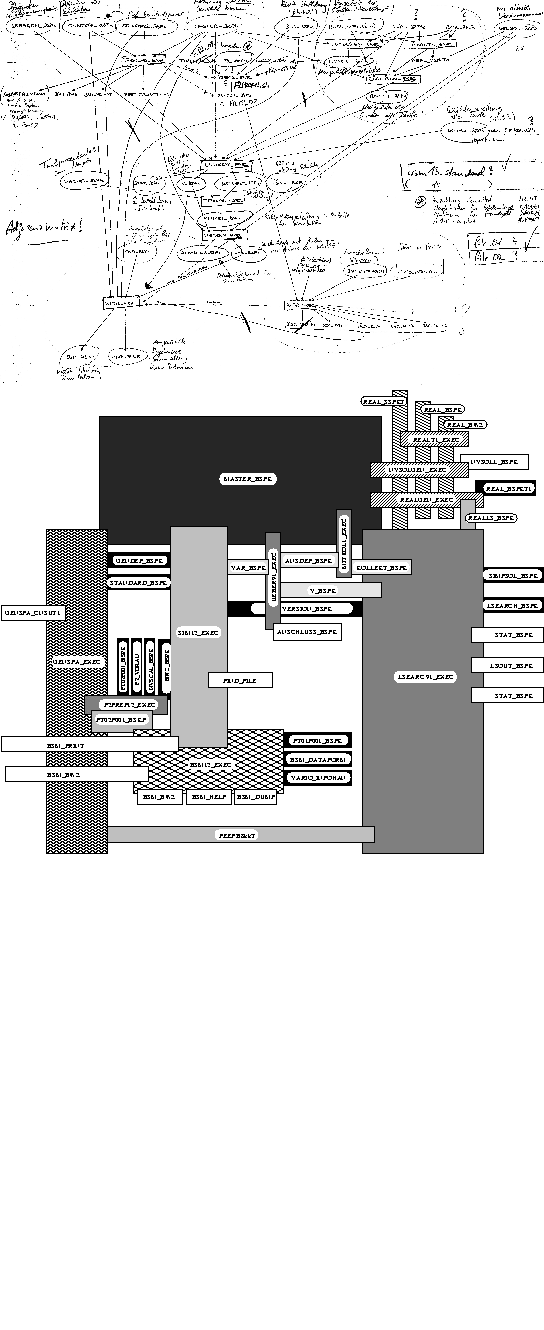
Seit vielen Jahrzehnten beschäftigen sich Graphentheoretiker mit Eigenschaften von diskreten mathematischen Strukturen. Mit zunehmendem Einsatz von Computern für Aufgaben in der Visualisierung von Daten ist das Interesse an algorithmischen Verfahren zur Darstellung von Graphen (,,Graph Drawing``) immer größer geworden.
Wie läßt sich ein Graph so zeichnen, daß die Zeichnung
möglichst einfach zu verstehen ist? Naturgemäß ist dies
keine scharf definierte Aufgabenstellung. Betrachtet man aber
Abbildung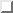 
, in der die Filestruktur eines
Systems zur Prognose der Bestandsentwicklung der Landesbausparkassen
dargestellt ist, so wird deutlich, wie wichtig es ist,
komplexe Graphen so
darzustellen, daß die wichtigen Informationen leicht ablesbar
sind.
Angesichts der Vielfältigkeit darzustellender Informationen
ist es nicht nur wichtig, Algorithmen zu untersuchen, sondern auch von
Bedeutung, neue Konzepte für die Darstellung von Graphen
zu entwickeln. Ein solches Konzept ist die sogenannte
,,Sichtbarkeitsdarstellung`` von Graphen. Dabei werden
Knoten durch Objekte im Raum repräsentiert, die miteinander
durch eine Kante verbunden sind, wenn sie sich auf wohldefinierte
Weise ,,sehen`` können. Je nach Art der Objekte und
Definition der Sichtbarkeit können recht unterschiedliche
Graphen dargestellt werden. Aufgrund ihrer einfachen Struktur
interessiert man sich besonders für Objekte wie achsenparallele
Quadrate, Rechtecke, Kreise, Würfel und Quader. Interessante
Versionen der Sichtbarkeit von zwei Objekten
sind dadurch gegeben, daß
es eine z-achsenparallele oder allgemein achsenparallele Verbindung eines
Paares von jeweils inneren Punkten gibt, die keine anderen Objekte
berührt. Abbildung zeigt die Struktur eines komplizierten
Softwarepaketes und eine Aufsicht auf
eine Repräsentierung; dabei entspricht die Größe der verwendeten
Rechtecke ungefähr der Wichtigkeit der dargestellten Files.
Die (gerichteten) Kanten sind (von unten nach oben) durch Überlappung
zweier Rechtecke repräsentiert. Input-Files sind schwarz dargestellt,
Output-Files weiß.
Welche Graphen lassen sich auf diese Weise repräsentieren? Bislang gibt es keine algorithmischen Methoden zur Berechnung einer Sichtbarkeitsdarstellung. Es lassen sich aber eine Reihe von mathematischen Aussagen darüber treffen, wo die Möglichkeiten solcher Darstellungen an ihre Grenzen stoßen. Mit Hilfe von kombinatorischen Methoden konnten wir obere und untere Schranken für die Größe von vollständigen Graphen mit Sichtbarkeitsdarstellungen finden.