Reihenfolgeplanungsprobleme behandeln die optimale Zuweisung von Aktivitäten an knappe Ressourcen im Zeitablauf. Aktivitäten können Arbeitschritte an einem Werkstück, Instruktionen in einem Computerprogramm, Verfahrensschritte in chemischen Prozessen usw. sein. Ressourcen sind etwa die Anzahl der zur Verfügung stehenden Arbeiter oder Werkbänke, Anzahl der Prozessoren, Hauptspeicherangebot, Betriebsmittel usw. Die Zuweisung von Aktivitäten im zeitlichen Ablauf wird durch einen Reihenfolgeplan (,,Schedule``) festgelegt. In einem Reihenfolgeplan wird jeder Aktivität ein oder mehrere Zeitintervalle auf einer oder mehreren Maschinen bzw. Ressourcen zugewiesen. Ein Reihenfolgeplan ist zulässig, wenn alle Nebenbedingungen eingehalten werden. Die Optimalitätskriterien können unterschiedlicher Natur sein, wie die Minimierung der Gesamtlaufzeit, die Minimierung der Summe der individuellen Fertigstellungszeiten (Durchlaufzeit), das Einhalten vorgegebener Fertigstellungszeiten usw.
Seit den fünfziger Jahren werden Reihenfolgeplanungsprobleme im Gebiet
des Operations Research untersucht.
Nicht nur die große Fülle an industriellen Anwendungen
(siehe z.B. Abschnitt 
)
macht diese Fragestellungen interessant. Aus der Sicht des Wissenschaftlers
bietet sich eine unüberschaubare Vielfalt leicht zu beschreibender,
aber bereits für kleine Instanzen sehr schwer zu lösender Aufgaben dar.
Eine theoretisch befriedigende Erschließung des gesamten
Gebietes der Reihenfolgeplanung ist bisher nicht
gelungen, selbst die Anpassung von Standardverfahren
(Dynamische Programmierung, Branch-and-Bound usw.) zur Lösung
von Spezialfällen ist nicht einfach, was die Vielzahl an
Publikationen dazu belegt.
Scheduling-Probleme lassen sich auf verschiedene Weisen als Probleme mit
Ganzzahligkeitsrestriktionen auffassen. Diese Ganzzahligkeitsbedingungen
erschweren i.a. das Finden einer optimalen Lösung.
Für die Anwendung von Verfahren der ganzzahligen Linearen
Optimierung auf Scheduling-Probleme
-- die in jüngster Zeit verstärkt untersucht werden --
ist eine problemadäquate und verfahrensgeeignete
Modellierung entscheidend.
Um mit Hilfe von Methoden der polyedrischen Kombinatorik
ein Optimierungsproblem
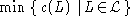über einer Menge 
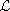von Reihenfolgeplänen zu lösen,
ordnet man jedem Reihenfolgeplan L
einen Vektor x(L) im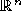 
(für geeignetes n) zu und studiert dann die
konvexe Hülle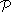 
der derart gebildeten Vektoren:
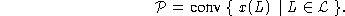
Die Suche nach linearen Beschreibungen dieser Polyeder
ist einer der wichtigsten Schritte für die Anwendung von
Verfahren der ganzzahligen Linearen Optimierung.
Vollständige lineare Beschreibungen, d.h. die Beschreibung
des Polyeders nur durch lineare Ungleichungen, ermöglichen
oft die polynomielle Lösbarkeit des untersuchten Problems
und über die Dualitätstheorie der Linearen Programmierung
die Herleitung von kombinatorischen Minimum-Maximum Aussagen.
Unvollständige
lineare Beschreibungen werden zur Gewinnung von Schranken in
den Verfahren der ganzzahligen Linearen Optimierung benutzt.
Wir haben uns vor allem mit dem deterministischen
Ein-Maschinen-Belegungsproblem unter gewissen Reihenfolgerestriktionen
beschäftigt.
Hier muß eine Menge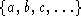 
von Aktivitäten
auf einer Maschine ausgeführt werden. Dabei kann die Maschine zu jeder
Zeit nur eine Aktivität ausführen, die Aktivitäten dürfen nicht
unterbrochen werden, und zwischen einigen Aktivitäten bestehen
Reihenfolgerestriktionen nach der Art: ,,a muß vor b ausgeführt werden``.
Gesucht wird nun ein Belegungsplan - eine vollständige Anordnung
der Aktivitäten -, der ein bestimmtes Zielkriterium optimiert.
Motivierend für das Studium dieser Strukturen sind Reihenfolgeplanungsprobleme mit der Zielfunktion ,,Minimierung der (gewichteten) Summe der individuellen Fertigstellungszeiten``. Hier wird in einem Belegungsplan jede Aktivität mit ihrer Fertigstellungszeit bewertet, der Wert des Belegungsplanes ist die Summe der (gewichteten) Fertigstellungszeiten. Im einfachen Fall konstanter Prozeßzeiten von einer Einheit entspricht die Fertigstellungszeit einer Aktivität genau ihrer Position im Belegungsplan, wenn der Maschine keine Leerlaufzeiten zugewiesen werden. Die mit den Belegungsplänen korrespondierenden Vektoren der Fertigstellungszeiten sind genau die mit der Partialordnung verträglichen Permutationen.
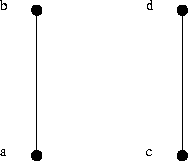
Abbildung: Eine einfache serienparallele Ordnung
Die vier Aktivitäten aus Beispiel mögen die Gewichte
(,,relative Wichtigkeit``)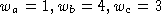 
und
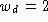und eine Laufzeit von jeweils einer Zeiteinheit haben. Eine optimaler
Plan wäre dann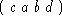 
mit einem Zielfunktionswert
von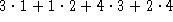 
.
Aufbauend auf früheren Arbeiten verschiedener Autoren zur konvexen Hülle der Fertigstellungszeitenvektoren haben wir durch Einführung supermodularer Funktionen auf serien-parallelen Partialordnungen erstmalig Supermodularität mit Reihenfolgerestriktionen verbunden. Sub- bzw. Supermodularität kann als diskretes Analogon der Konvexität verstanden werden. Sehr viele kombinatorische Optimierungsprobleme haben grundlegend eine sub- oder supermodulare Natur, mit dieser Erkenntnis können sie vielfach gelöst werden. Das Polytop der so erzielten Inzidenzvektoren linearer Erweiterungen stellt deshalb eine Verallgemeinerung wie auch eine Vereinheitlichung des Permutaeders von serien-parallelen Ordnungen und des Basispolyeders supermodularer Funktionen auf ungeordneten Mengen dar. Wir konnten für einige wichtige Problemklassen eine vollständige polyedrische Beschreibung finden. Durch die Erweiterung des Greedy-Algorithmus von ungeordneten Mengen auf partielle Ordnungen haben wir das Verfahren von Sidney (1975) der rekursiven Wahl rho-maximaler Ideale zur Lösung des Reihenfolgeplanungsproblems strukturell erklären können.
Mathematisch läßt sich die Situation wie folgt beschreiben:
Sei P = ( P, < ) eine partiell geordnete Menge und
g eine supermodulare Funktion auf den Idealen von P.
Jeder linearen Erweiterung
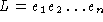von P ordnen wir durch
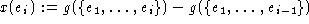einen Inzidenzvektor 
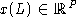zu.
Die konvexe Hülle der Inzidenzvektoren aller
linearen Erweiterungen von P bildet das Basispolyeder
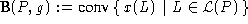von P und g. Die supermodulare Funktion g
heißt kompatibel mit P, wenn für alle
seriell-reduzierbaren konvexen Mengen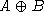 
in P und alle Ideale 
,
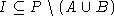für die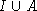 
und
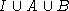auch Ideale sind, der Term
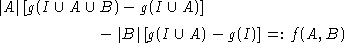
konstant (unabhängig von I) ist. Eine Teilmenge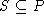 
heißt konvex, wenn für alle Elemente x < z aus S auch alle
Elemente ,,dazwischen``, d.h. x < y < z, in S enthalten sind.
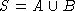ist seriell-reduzierbar, wenn alle Elemente von B
über allen Elementen von A liegen.
Das Hauptergebnis lautet nun:
Die Entwicklung und das Studium dieser Polyeder ist durch die Zielfunktion ,,Minimierung der Summe der ordnungsinduzierten Rüstkosten`` motiviert. Folgen in einem Belegungsplan zwei Aktivitäten e und f unmittelbar aufeinander, die keiner Reihenfolgerestriktion unterliegen, oder ist f die erste Aktivität, so werden Rüstkosten bei f notwendig. Die Rüstkosten hängen dabei nur von f ab. Ist der unmittelbare Vorgänger von f im Belegungsplan ein notwendiger Vorgänger, so fallen keine Rüstkosten an. Der Wert des Belegungsplanes ist die Summe der angefallenen Rüstkosten. Bei reihenfolgeunabhängigen Prozeßzeiten und nichtnegativen Rüstkosten (Rüstzeiten) entspricht die Rüstkostenminimierung der Minimierung der maximalen Fertigstellungszeit.
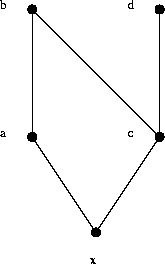
Abbildung: Eine Partialordnung mit einem isolierten N
In Beispiel mögen die Aktivitäten x, b, c und d jeweils
Rüstkosten eins haben, die Aktivität a habe Rüstkosten von drei.
Dann hat der Reihenfolgeplan 
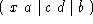insgesamt
Rüstkosten drei. Der Reihenfolgeplan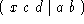 
trägt
Rüstkosten von vier, obwohl nur zwei anstelle von drei Rüstschritten
notwendig sind.
Schon der Spezialfall konstanter Rüstkosten einer Einheit ist ein NP-schweres Problem, das sogenannte Sprungzahlproblem. Interessanterweise ist der Spezialfall konstanter Rüstkosten von minus eins polynomiell lösbar. Das Sprungzahlproblem wird seit fast 30 Jahren untersucht und manchmal zu Unrecht zu den irregulären Problemen gezählt, die wenig oder gar keine strukturellen Erkenntnisse zulassen. Die bekannten polyedrischen Modelle aus der Reihenfolgeplanung bilden das Rüstproblem nicht zufriedenstellend ab, da sie die Gutartigkeit bestimmter Klassen von Reihenfolgerestriktionen nicht berücksichtigen oder aber keine Lineare Optimierung ermöglichen. Wir haben hier zum ersten Mal ein allgemeines Modell für beliebige Rüstkosten aufgezeigt und dann eine vollständige polyedrische Beschreibung für serien-parallele und N-dünne Ordnungen entwickelt.
Dieser neue polyedrische Ansatz für ordnungsinduzierte Rüstprobleme kann in folgender Weise beschrieben werden:
Zu jeder linearen Erweiterung L einer partiellen Ordnung P
definieren wir den 0-1-Inzidenzvektor 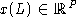durch
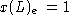genau dann, wenn der unmittelbare Vorgänger des
Elementes e in der linearen Erweiterung L kein Vorgänger
von e in der Partialordnung P ist oder wenn e das erste Element
in L ist. Diese Zuordnung ist i.a. nicht injektiv.
Das Rüstpolyeder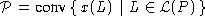 
ist die konvexe Hülle der Inzidenzvektoren
aller linearen Erweiterungen von P.
Hier lautet ein Hauptergebnis:
(Dabei heißt eine Teilmenge 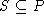heißt bipartit, wenn sie keine
drei Elemente x < y < z enthält.)
Die Ganzzahligkeit des Polyeders konnte mit einem ,,Box-TDI``-System
gezeigt werden. Daneben mußte auch zu einem gegebenem 0-1-Vektor
die Existenz einer passenden linearen Erweiterung nachgewiesen werden.
Durch eine Erweiterung auf lokale N-Strukturen haben
wir dann die vollständige lineare Beschreibung des
Rüstpolyeders von N-dünnen Ordnungen hergeleitet.
Im Gegensatz zu serien-parallelen Ordnungen ist hier
das Rüstproblem selbst mit nichtnegativen Rüstkosten
nicht mit dem Greedy-Algorithmus (,,Beginne mit einem beliebigen
zulässigen Element und fahre mit einem teuersten Nachfolger des
zuletzt gewählten Elementes fort, wenn dies möglich ist, anderenfalls
wähle ein beliebiges zulässiges Element``) lösbar.
Eines der interessanten offenen Probleme ist das Erkennungsproblem für Inzidenzvektoren von linearen Erweiterungen beliebiger Partialordungen:
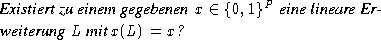
Interessant, schwer und bisher unbeantwortet ist auch die Frage nach der Aufnahme individueller Fertigstellungszeiten in dieses Modell, das die Minimierung der Durchlaufzeiten ermöglichen könnte.