

Next: Erfahrungen und Ergebnisse
Up: Turbulenzsimulation auf Parallelrechnern
Previous: Modellbildung
Auf den Vektorrechnern der DLR werden zur Zeit Produktionsläufe mit
Auflösungen von 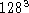 Punkten im täglichen Betrieb
durchgeführt. Mit einer dabei erreichten Rechenleistung von circa
150 MFlop/s und einem
Speicherbedarf von einem halben Gigabyte benötigt eine solche
Simulation 4 Stunden CPU Zeit auf einem Prozessor der Cray Y-MP. Der
Grad der
Turbulenz der so simulierten Strömung (gemessen als Reynoldszahl) ist
jedoch im Vergleich zu atmosphärischen Strömungen zu gering. Eine
entscheidende Verbesserung
ist durch eine Verfeinerung des Gitters möglich. Die dafür
notwendige Rechenleistung steht heutzutage nur auf
Parallelrechnern zur Verfügung. Aus diesem Grunde wurde vor zwei
Jahren mit der Parallelisierung des Programms begonnen.
Punkten im täglichen Betrieb
durchgeführt. Mit einer dabei erreichten Rechenleistung von circa
150 MFlop/s und einem
Speicherbedarf von einem halben Gigabyte benötigt eine solche
Simulation 4 Stunden CPU Zeit auf einem Prozessor der Cray Y-MP. Der
Grad der
Turbulenz der so simulierten Strömung (gemessen als Reynoldszahl) ist
jedoch im Vergleich zu atmosphärischen Strömungen zu gering. Eine
entscheidende Verbesserung
ist durch eine Verfeinerung des Gitters möglich. Die dafür
notwendige Rechenleistung steht heutzutage nur auf
Parallelrechnern zur Verfügung. Aus diesem Grunde wurde vor zwei
Jahren mit der Parallelisierung des Programms begonnen.
In einem gemeinsamen Projekt des Zentrums für Paralleles Rechnen an
der Universität zu Köln und
der DLR wurde das Simulationsprogramm so umgestaltet, daß es jetzt
auf einem breiten Spektrum von Parallelrechnern einsetzbar ist. Durch
die Verwendung der portablen Kommunikationsbibliothek MPI, die den
Datenaustausch zwischen den Prozessoren des Parallelrechners regelt,
ist es möglich, das Programm in kürzester Zeit auf
verschiedenen parallelen Architekturen zu implementieren. Dadurch
konnten Höchstleistungsrechner mehrerer Anbieter
miteinander verglichen werden.
Die Parallelisierung basiert auf dem Konzept der
Datendekomposition. Dabei bearbeitet jeder Prozessor einen ihm
zugeordneten Datenbereich und tauscht gegebenenfalls zusätzliche
Informationen mit den restlichen Prozessoren aus. Durch eine doppelte
Berechnung der Daten auf den Grenzschichten der einzelnen Bereiche
können mit dieser Methode große Teile jedes Integrationsschrittes
ohne weitere Kommunikation durchgeführt werden.
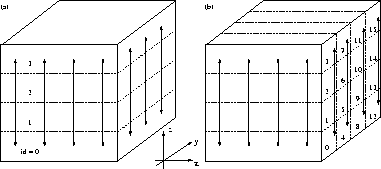
Abbildung: Datendekomposition: (a) eindimensional und (b)
zweidimensional. Die Pfeile bezeichnen die Verteilung der
tridiagonalen Gleichungssysteme.
Während der für inkompressible Strömungen notwendigen globalen
Druckkorrektur sind eine zweidimensionale Fouriertransformation (FFT) und
die Lösung tridiagonaler Gleichungssysteme erforderlich. Die
zweidimensionale FFT kann als eine Folge von eindimensionalen
Transformationen betrachtet werden, die jeweils autark auf den Daten eines
Prozessors durchgeführt werden sollten. Aus diesem Grunde teilen wir
das Simulationsgebiet in waagerechte Quader auf, die in x-Richtung
über die gesamte Breite des Gebietes reichen. Nach der
ersten eindimensionalen FFT (in x-Richtung) wird das Feld
transponiert und die zweite FFT in y-Richtung durchgeführt.
Eine sogenannte eindimensionale Aufteilung in horizontale Scheiben
bietet zwar den Vorteil, die gesamte 2D-FFT ohne Datentransposition
berechnen zu können, jedoch entstehen dabei zu wenige Teilgebiete, um sie
auf massiv-parallelen Rechnern mit bis zu 512 Prozessoren auf die
Knoten verteilen zu können.
Nach der Fouriertransformation sind tridiagonale Gleichungssysteme zu
lösen, die wie in Abbildung  angedeutet verteilt
sind. Hierfür haben wir ein neues Verfahren entwickelt, welches auf
einer Divide-and-conquer-Strategie basiert. Jeder Prozessor löst
dabei in einem ersten Schritt die ihm zugeordneten Teile des
Systems. Mit den Lösungen eines
globalen Korrektursystems werden anschließend die Teillösungen
korrigiert.
angedeutet verteilt
sind. Hierfür haben wir ein neues Verfahren entwickelt, welches auf
einer Divide-and-conquer-Strategie basiert. Jeder Prozessor löst
dabei in einem ersten Schritt die ihm zugeordneten Teile des
Systems. Mit den Lösungen eines
globalen Korrektursystems werden anschließend die Teillösungen
korrigiert.



Next: Erfahrungen und Ergebnisse
Up: Turbulenzsimulation auf Parallelrechnern
Previous: Modellbildung
Webmaster
<www@zpr.uni-koeln.de>, 7. Apr. 1997
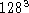 Punkten im täglichen Betrieb
durchgeführt. Mit einer dabei erreichten Rechenleistung von circa
150 MFlop/s und einem
Speicherbedarf von einem halben Gigabyte benötigt eine solche
Simulation 4 Stunden CPU Zeit auf einem Prozessor der Cray Y-MP. Der
Grad der
Turbulenz der so simulierten Strömung (gemessen als Reynoldszahl) ist
jedoch im Vergleich zu atmosphärischen Strömungen zu gering. Eine
entscheidende Verbesserung
ist durch eine Verfeinerung des Gitters möglich. Die dafür
notwendige Rechenleistung steht heutzutage nur auf
Parallelrechnern zur Verfügung. Aus diesem Grunde wurde vor zwei
Jahren mit der Parallelisierung des Programms begonnen.
Punkten im täglichen Betrieb
durchgeführt. Mit einer dabei erreichten Rechenleistung von circa
150 MFlop/s und einem
Speicherbedarf von einem halben Gigabyte benötigt eine solche
Simulation 4 Stunden CPU Zeit auf einem Prozessor der Cray Y-MP. Der
Grad der
Turbulenz der so simulierten Strömung (gemessen als Reynoldszahl) ist
jedoch im Vergleich zu atmosphärischen Strömungen zu gering. Eine
entscheidende Verbesserung
ist durch eine Verfeinerung des Gitters möglich. Die dafür
notwendige Rechenleistung steht heutzutage nur auf
Parallelrechnern zur Verfügung. Aus diesem Grunde wurde vor zwei
Jahren mit der Parallelisierung des Programms begonnen.