Konjugiertes Gradientenverfahren für quadratische Funktionen
Im Fall einer quadratischen Funktion der Gestalt
Für das konjugierte Gradientenverfahren wählen wir zunächst einen Startpunkt
Wir nehmen an, dass
Dann gibt es eine Richtung
Wir untersuchen nun das Verhalten von
Dazu betrachten wir die Funktion einer Variablen
Ist
Man nennt
Ist
Eine sinnvolle Wahl für die Schrittweite ergibt sich, wenn man
Wir setzen nun
Es ist offensichtlich, dass
Beispiel: Zur Minimierung der Funktion
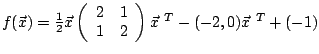
Der Gradient an dieser Stelle ist
D.h. wir berechnen das Minimum der Funktion
welches wir in der Nullstelle
Wir erhalten einen neuen Iterationspunkt
Als nächstes müssen wir ein zu
Man kann zeigen, dass der neue Iterationspunkt
Ein zu
Zusammenfassend erhalten wir den folgenden Algorithmus:
|
Wegen
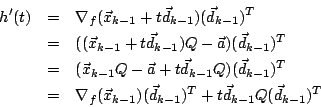
erhält man die (eindeutig bestimmte) exakte Schrittweite
Man erhält also wie gewünscht einen Wert grösser Null für
Beispiel (Fortsetzung):
Unser neuer Iterationspunkt ist nun
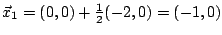 .
.
Der Gradient an dieser Stelle ist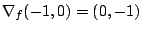 .
.
Für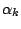 berechnen wir
berechnen wir
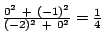 und müssen nun
und müssen nun 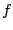 von
von 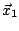 aus
aus
in die zu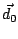 konjugierte Richtung
konjugierte Richtung
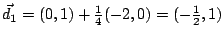 minmieren,
minmieren,
d.h. das Minimum der Funktion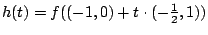 bestimmen.
bestimmen.
Dazu berechnen wir die Nullstelle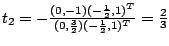 der ersten Ableitung
der ersten Ableitung 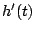 .
.
Der Punkt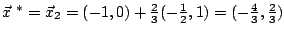 ist dann das gesuchte strenge Minimum von
ist dann das gesuchte strenge Minimum von 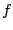 .
.
Der Gradient an dieser Stelle ist
Für
in die zu
d.h. das Minimum der Funktion
Dazu berechnen wir die Nullstelle
Der Punkt