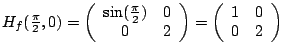Optimalitätskriterien
Man nennt ein Tupel
Eine
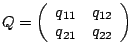
Dies ist der Fall, falls
Notwendiges Kriterium:
Ist
Hinreichendes Kriterium:
Ist
Die hinreichenden Bedingungen für ein strenges lokales Minimum sind jedoch nicht notwendig. Der kritische Punkt
|
|
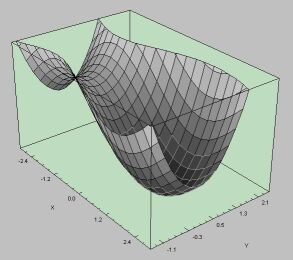 |
Bemerkung:
Für den Fall von nur einer Veränderlichen entsprechen diese Optimalitätskriterien denen der aus der Differentialrechnung bei einer Veränderlichen bekannten: "
Da im Fall einer quadratischen Funktion
|
Beispiel: |
Die quadratische Funktion |
|
|
|
|
mit positiv definiter Matrix |
|
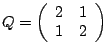 |
|
|
besitzt ein strenges Minimum an der kritischen Stelle |
|
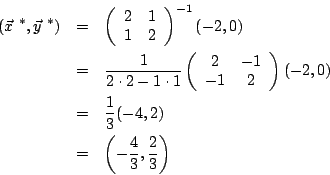 |
Wir werden zeigen, wie man mit dem konjugierten Gradientenverfahren das strenge Minimum
Auf diese Weise kann die bei mehreren Veränderlichen aufwendige Berechnung der inversen Matrix