1.1 Differenzengleichungen

Mit Differenzengleichung lassen sich Änderungen von Zustandsgrößen mit der Zeit beschreiben. Im Unterschied zu Differentialgleichungen wird dabei nicht davon ausgegangen, dass diese Veränderungen kontinuierlich erfolgen, sondern es werden nur die Übergänge von Zeitpunkt t zum Zeitpunkt betrachtet.

Im folgendem wird aus Gründen der Einfachheit auf 1 gesetzt. Tritt X(t) auf der rechten Seite der Gleichung nur mit der Potenz 1 auf, dann ist die Differenzengleichung linear. Alle anderen Differenzengleichungen heißen nichtlinear.

Sparen mit Verzinsung

Als Beispiel kann man einen Sparer betrachten, der monatlich zum Ersten seine Sparrate auf ein Sparkonto einzahlt. Sein Guthaben wird ihm verzinst. Um die Rechnung möglichst einfach zu halten, nehmen wir an, dass diese Verzinsung ebenfalls monatlich allerdings zum Monatsende erfolgt. Damit ist auch seine Spargeldeinzahlung einen gesamten Monat auf dem Konto. Den Zinssatz pro Monat bezeichnen wir mit p und berechnen damit den Aufzinsungsfaktor q. Der Aufzinsungsfaktor entspricht einfach dem Faktor mit dem man das Kapital multiplizieren muss, um das des nächsten Zeitpunktes zu bestimmen. Ist also p in Prozent gegeben, dann gilt q=1+p/100. Weiterhin gehen wir davon aus, dass er eine gleichbleibende Rate r zahlt. Nehmen wir an, dass der Sparer mit einen Kapital startet. Betrachten wir, wie sich das Kapital am Anfang verändert

Wegen folgt

Exponentielles Wachstum und Zerfall

Betrachten wir einen anderen Vorgang, die exponentielle Wachstumsgleichung.
X(t+1)=rX(t)
mit dem Startwert .
Auch diese Gleichung lässt sich sehr leicht lösen:
.
Sie lässt sich andererseits sehr gut dafür nutzen, zu zeigen wie man durch die Änderung eines Parameters ein vollkommen unterschiedliches Verhalten einundderselben Grundgleichung erreichen kann.
Man sieht, dass X(t) nur dann wachsen kann, wenn |r|;SPMgt;1 gilt. Oder genauer, wir betrachten

• r ;SPMgt;1 :
  X(t) wächst exponentiell an.
• r =1 :
  X(t) bleibt auf dem Anfangswert stehen.
• 0;SPMlt; r ;SPMlt; 1 :
  X(t) nimmt exponentiell ab und erreicht schließlich die Null.
• r ;SPMlt; -1 :
  X(t) wechselt sein Vorzeichen alternierend und wächst an, bzw. die Amplituden verstärken sich.
• -1 ;SPMlt; r ;SPMlt;0:
  Auch hier wechselt X(t) sein Vorzeichen, pendelt sich aber um die Null ein.

Ähnliches gilt auch für kompliziertere Fälle.

Logistische Abbildung

Die logistische Abbildung gleicht formal der logistischen Wachstumsgleichung. Wenn man die kontinuierliche Wachstumsgleichung mit dem Eulerverfahren diskretisiert, dann ergibt sich als Ergebnis die log. Abbildung. Sie lässt sich aber im Gegensatz zu der anderen Gleichung nicht mehr analytisch lösen.

Dafür kann sie in Abhängigkeit von r noch unterschiedlicheres Verhalten bis hin zum Chaos zeigen. Um das Verhalten der log. Abbildung näher zu untersuchen geht man ähnlich vor, wie bei Differentialgleichungen. Man kann zu einem die stationären Lösungen bestimmen. Zum anderen könnte man die Gleichung vom Computer bis zu einem Zeitpunkt ausrechnen lassen.

Stationäre Lösungen: Fixpunkte

Stationäre Lösungen von Differenzengleichungen sind ähnlich wie bei Differentialgleichungen die Punkte, bei denen keine Veränderungen mehr erfolgen. Keine Veränderung bei Differenzengleichungen heißt, dass X(t+1)=X(t) gilt. Mit dieser Bedingung lassen sich die stationären Lösungen, die bei Differenzengleichungen auch Fixpunkte genannt werden, bestimmen. Als erstes Beispiel betrachten wir die exp. Gleichung:

Bedingung: . Die Bedingung ist offensichtlich erfüllt, wenn: a) oder b) r=1 ist. Beide Lösungen sind offensichtlich. Wenn kein X vorhanden ist, dann kann es sich auch nicht verändern. Oder wenn die Wachstumsrate eins ist, ist ebenfalls jede Veränderung ausgeschlossen. Die exponentielle Wachstumsgleichung ist ein lineares System. Hier kann nur ein Fixpunkt vorliegen (außer bei r=1), der entweder stabil oder instabil ist. Anders sieht das bei nichtlinearen Differenzengleichungen aus.

hat zwei Gleichgewichtspunkte: oder .

Stabilität von Fixpunkten

Um die Stabilität zu untersuchen, geht man ähnlich wie bei den Differentialgleichungen vor. Wie haben die Ausgangsgleichung:

mit den Fixpunkt . Zuerst führt man wieder einen Störungsterm . Gilt nun, dass gegen Null strebt, wenn t immer größer wird, dann ist stabil. Zunächst einmal formen wir den Ausdruck oben ein wenig um. . Damit haben wir dasselbe für . Wie setzen beiden Ausdrücke in die Differenzengleichung von oben ein

und führen wieder die Taylorreihenentwicklung durch.

Da (Fixpunkt!) bekommt man:

Damit heben wir die exp. Wachstumsgleichung und können folgendes Verhalten erkennen:
Nur für ist das System stabil. Gilt , dann kann man Schwingungen feststellen. wird als kritischer Punkt bezeichnet.
Als Beispiel wird die Stabilität der beiden Fixpunkte der log. Wachstumsgleichung berechnet.
Zunächst einmal berechnet man die Ableitung von f(X(t)) nach X(t).

1)
Damit: . Damit ist dieser Gleichgewichtspunkt instabil, sobald der Wachstumsparameter vom Betrage her eins überschreitet.
2)
Es ist

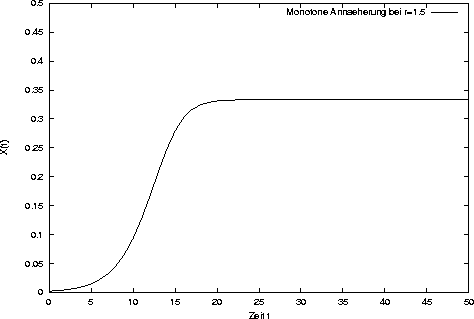
Gilt r;SPMlt;0, dann ist der zweite Fixpunkt instabil. Stabil ist er für den Bereich 1;SPMlt;r;SPMlt;3. Dabei zeigt er folgendes Verhalten. Bis zum Wert 2 bewegt sich X(t) monoton auf den Gleichgewichtspunkt zu. Bei einem Wert größer als 2 hingegen fängt es an zu schwingen.

Zyklen

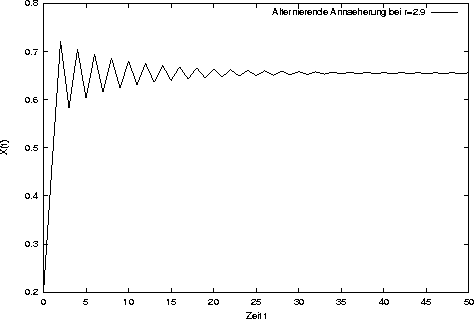
Zyklen in einem System treten auf, wenn periodische Schwingungen vorliegen. Das heißt nach einer bestimmten Zeitspanne wird der Punkt genau wieder erreicht und das System beginnt von vorne. Zyklen werden unterschieden nach ihrer Periode, d.h. nach der Zeit, die sie brauchen, um wieder in den Ausgangspunkt zurückzukehren. Fixpunkte sind gewissermaßen Zyklen mit der Periode eins. Die formale Definition eines Zyklus mit der Periode k lautet:

Oben bei der logistischen Abbildung, war erwähnt worden, dass der zweite Fixpunkt instabil wird, sobald der Wachstumsparameter die 3 überschreitet. Man kann jetzt zeigen, dass der Fixpunkt gewissermaßen von einem Zyklus mit der Periode 2 abgelöst wird.

Die Vorgehensweise ist wie bei einem Fixpunkt. Man hat die Forderung:1:X(t+2)=X(t), und 2:X(t+1)!=X(t). Damit muss man alle Punkte berechnen, die die erste Gleichung erfüllen. Danach setzt man sie in die zweite ein und nimmt schließlich alle Punkte, die diese nicht erfüllen. Die Rechnung führt hier auf ein Polynom dritter Ordnung und wird hier nicht durchgeführt. Auch die Stabilität (lokal) von Zyklen kann man wieder mit der Taylorreihe und dem Störungsterm zeigen. Die Ausbildung eines periodischen Verhaltens bei der log. Abbildung ist hier ein erster Schritt zum chaotischen Verhalten der Gleichung.

Wege ins Chaos

Mit dem Begriff Chaos wird zumeist folgendes Verhalten umschrieben.

• Das System zeigt ein aperiodisches beschränktes Verhalten. Aperiodisch heißt, das das System keinen Punkt zweimal durchläuft. Die Bedingung der Beschränkheit bedeutet, dass das System in einem abgrenzbaren Raum bleibt.
• Das Lösungsverhalten ist stark abhängig von Ausgangswerten. Startet das System mit zwei sehr ähnlichen Werten, dann verlaufen die Lösungen trotzdem nicht nahe beieinander.

Wenn man bei der log. Abbildung dem Wert von r weiter nach oben verschiebt, dann kann man folgendes erreichen. Sobald der Wert von r die 3 überschreitet, beginnt ein periodisches Verhalten.

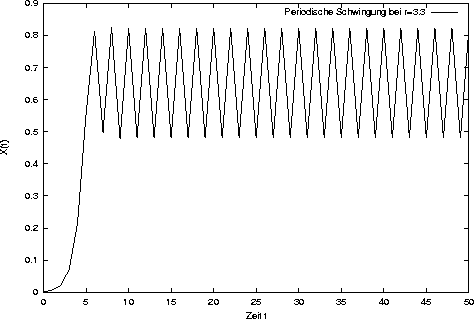
Zunächst noch mit der Periode 2, d.h. nach zwei Zeitschritten ist das System wieder im Ausgangspunkt. Wie man erkennt, werden damit quasi zwei Eckpunkte immer wiederholt. Vergrößert man den Wert von r weiter, beginnen sich die Perioden zu verdoppeln. Bei einem Wert größer als 3.4495 liegt bereits Periode 4 vor. Periode 8 tritt bei 3.5441 auf, Periode 16 bei 3.5644, danach, bis die 3.57 erreicht wird, verdoppelt sich die Periode immer weiter, wobei die Abstände immer kürzer werden.

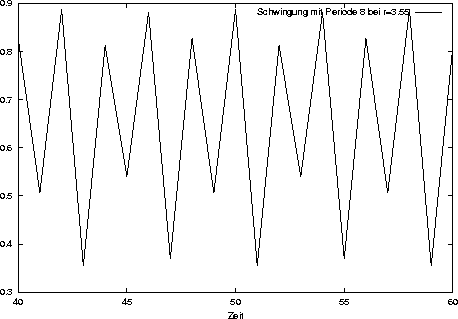
Feigenbaum konnte zeigen, dass die Längen zweier aufeinander folgender Intervalle miteinander in Beziehung stehen.

Die Konstante wird nach ihm Feigenbaum-Konstante genannt und gilt für alle Intervalle bei Periodenverdoppelung.
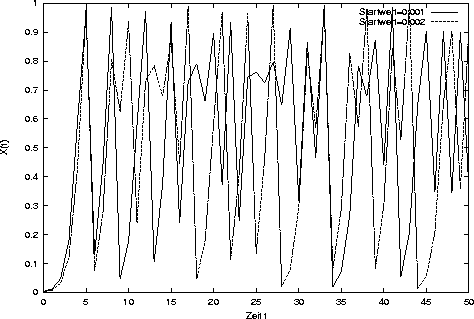
Bei einem Wert von 3.57 schließlich kippt das System ins Chaos. Es tritt erst einmal kein periodisches Verhalten mehr auf. In der folgendem Abbildung wurden die Werte von X(t) für zwei unterschiedliche Startwerte über 50 Zeitschritte hinweg aufgetragen. Man erkennt, dass keine regelmäßigen Schwingungen mehr auftreten. Zudem verhalten sich die beiden Kurven sehr unterschiedlich, obwohl die Startwerte nur um 0.001 auseinander liegen.

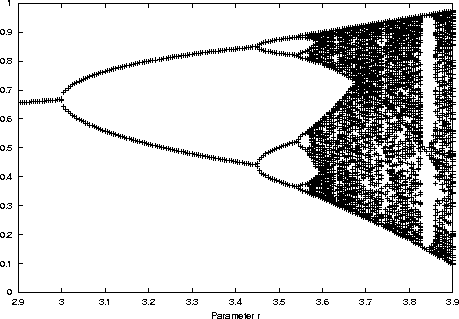
Ein interessantes Phänomen ist, dass sich für größere Werte von r für kurze Abschnitte Fenster mit periodischen Verhalten ausbilden. In der folgenden Abbildung wurden die stationären Punkte von X(t) gegen den Wachstumsparameter r aufgetragen. Periodenverdoppelungen erkennt man an den Gabelungen, die auch Bifurkationen genannt werden.
Die Lücken in der Abbildung sind die Fenster, in denen wieder periodisches Verhalten auftritt.