Mikroskopische Verkehrsflußmodelle

Anknüpfend an unsere Untersuchungen des CA-Modells nach Nagel und Schreckenberg wurden in einer Dissertation und einer unterstützenden Diplomarbeit die phänomenologischen Eigenschaften verschiedener mikroskopischer Verkehrsflußmodelle genauer analysiert. Dabei wurde ein neues Fahrzeugfolgemodell entwickelt, das inzwischen auch standardmäßig in unserer Simulationssoftware PLANSIM-T Anwendung findet.

Ausgangspunkt der Betrachtungen waren empirische Untersuchungen zur Dynamik des Verkehrsflusses durch Kerner und Rehborn. Dort wurde nachgewiesen, daß Straßenverkehr in drei qualitativ verschiedenen Zuständen, nämlich dem Zustand des freien Verkehrs, des synchronisierten Verkehrs und des Staus vorgefunden werden kann. Die Übergänge zwischen verschiedenen Verkehrszuständen wurden als Phasenübergänge erster Ordnung interpretiert.

Staus sind, abgesehen von ihrer offensichtlichen Eigenschaft, einen Verkehrsfluß hoher Dichte und niedriger Geschwindigkeit zu besitzen, durch folgende Eigenschaften charakterisiert:

1.

Staus können auch in Abwesenheit irgendwelcher Hindernisse entstehen und lange Zeit existieren.

2.

Der Fluß aus dem Stau ist deutlich niedriger als der maximale Fluß.

3.

Der Fluß aus dem Stau ist stabil.

4.

Der Fluß aus dem Stau und die Geschwindigkeit der flußabwärtigen Staufront hängen nicht vom Fluß in den Stau ab.

5.

Es gibt metastabile Zustände hohen Flusses.

Ziel war nun die Abbildung der qualitativen und quantitativen Eigenschaften des Verkehrs, basierend auf einer Simulation der Dynamik einzelner Fahrzeuge. Bei der Modellierung der Einzelfahrzeugdynamik wird auf einen minimalen Satz von Regeln zurückgegriffen, der aus wenigen Grundannahmen über den Verkehrsfluß abgeleitet wird. Diese Grundannahmen sind: 1) Geschwindigkeit und Beschleunigung der Fahrzeuge sind begrenzt. 2) Die Wechselwirkung von Fahrzeugen führt zur kollisionsfreien Bewegung im Verkehr. 3) Jedes Fahrzeug bewegt sich (von stochastischen Fluktuationen abgesehen) mit der höchsten Geschwindigkeit, die mit obigen Restriktionen kompatibel ist. Aus diesen Annahmen wurde eine Familie von Modellen abgeleitet, die jeweils durch einen geschwindigkeitsabhängigen Wunschabstand und eine geschwindigkeitsabhängige Relaxationszeit der Fahrdynamik charakterisiert sind.

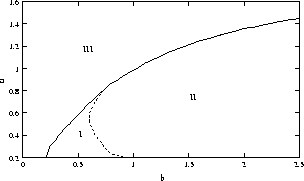
Eine Spezialisierung dieser Modellfamilie führt auf eine Unterfamilie, die durch die freien Parameter a und b, die typische Beschleunigungs- bzw. Verzögerungsfähigkeiten der Einzelfahrzeuge bezeichnen, charakterisiert wird. Je nach Wahl der freien Parameter a und b und der Maximalgeschwindigkeit der Fahrzeuge $v_{\rm max}$ zeigt das Modell drei qualitativ unterschiedliche Verhaltensweisen, die durch eine Einteilung der Modellfamilie in drei Klassen phänomenologisch jeweils gleichartiger Modelle charakterisiert wird.

• Klasse I:
  • a und b bezüglich empirisch bekannter Fahrdynamik realistisch, langreichweitige Wechselwirkung.
  • Alle o.g. Eigenschaften des Staus werden korrekt abgebildet.
  • Der Übergang in den gestauten Zustand ist ein Phasenübergang.

    
    

      

    Abbildung 4.3: Staubildung in Klasse I (Weg-Zeit-Diagramm))

    
    
    

• Klasse II:
  • b groß, kurze Bremswege, kurzreichweitige Wechselwirkung.
  • Eigenschaften 2, 3 und 5 der Staus werden nicht abgebildet.
  • Der Übergang in den gestauten Zustand ist kein Phasenübergang.

  
  

    

  Abbildung 4.4: Staubildung in Klasse II (Weg-Zeit-Diagramm))

  
  
  

• Klasse III:
  • a groß, Beschleunigung begrenzt Fahrdynamik nicht wesentlich.
  • System bildet keine Staus.

Phänomenologisch gesehen sind der Klasse I neben dem neuentwickelten Modell auch das makroskopische Kerner-Konhäuser-Modell, neuere Zellularautomatenmodelle und mit Einschränkungen auch das Optimal-Velocity-Model von Bando zuzuordnen. Klassische CA-Modelle des Verkehrsflusses, wie das Nagel-Schreckenberg-Modell sind den Klassen II und III zuzuordnen.

  

Abbildung: Grenzlinien der Modellklassen im (a,b)-Parameterraum (a = Beschleunigungsvermögen, b = Bremsvermögen der Fahrzeuge.)

Für eine praktische Anwendung, beispielsweise im Bereich des Verkehrsmanagements auf Schnellstraßen, sind nur Modelle der Klasse Igeeignet, weil die anderen beiden Klassen die Dynamik der Stauentwicklung falsch oder gar nicht abbilden. Die Update-Regeln für das im Rahmen unserer Forschung entwickelte Modell sind fast so einfach wie die der klassischen CA-Modelle, allerdings verwendet es kontinuierliche Ortskoordinaten x und Geschwindigkeitswerte v. Für jeden Zeitschritt werden die folgenden Operationen durchgeführt:

$$\begin{array}{lcl} v_{\rm des} &\leftarrow& min[v_{\rm max},... ..., v_{\rm des}]]\; ,\\ [2ex] x &\leftarrow& x + v, \end{array}$$

Hierbei bezeichnet $v_{\rm max}$ die Maximalgeschwindigkeit jedes einzelnen Fahrzeugs, $\epsilon\in[0,1]$ eine Modellkonstante und rand[s,t] eine Zufallszahl im Intervall [s,t]. Die maximale Geschwindigkeit $v_{\rm safe}$, bei der Kollisionen vermieden werden, berechnet sich als

$$v_{\rm safe} = v_{\rm l} + \frac{g - v_{\rm l}\tau} {\frac{v}{b} + \tau}\; .$$

aus der Geschwindigkeit des vorausfahrenden Fahrzeugs $v_{\rm l}$, dem Abstand g zum Vordermann und der Reaktionszeit $\tau$.

Dieses Modell für den Einspurverkehr läßt sich in einfacher Weise unter Wahrung der qualitativen Modelleigenschaften auf Mehrspurverkehr verallgemeinern. Nach dieser Verallgemeinerung wird eine exzellente quantitative Übereinstimmung der Modelleigenschaften mit empirisch ermittelten Daten der Verkehrsdynamik erreicht.