Dispersionsprobleme

Während es bei Packungsproblemen darum geht, möglichst viele Objekte auf möglichst kleinem Raum unterzubringen, ist bei Dispersionproblemen das Ziel, die Objekte möglichst weit voneinander entfernt zu plazieren. Fragestellungen dieser Art treten auf, wenn sich die Objekte so wenig wie möglich gegenseitig stören sollen, etwa bei Rundfunksendern oder Zweigstellen einer Ladenkette. Dispersionsprobleme lassen sich auch als Packungsprobleme modellieren, bei denen man eine fixe Anzahl von möglichst großen Objekten zu plazieren hat. Vom mathematischen Standpunkt sind fast alle dieser Probleme NP-schwer, d.h. es ist nicht damit zu rechnen, daß es einen exakten Algorithmus mit schneller Laufzeit gibt.
Hochbaum und Maass stellten 1985 ein polynomielles Approximationsschema vor, das für einen bestimmten Typ von Packungsproblemen schnelle Approximationsalgorithmen mit Gütegarantie beliebig nahe bei 1 liefert. Demgegenüber war für Dispersionsprobleme ein derartiges Schema nicht bekannt und es war unklar, ob es solch ein Schema überhaupt geben könne. Es gelang uns, diese offene Frage zu lösen, indem wir zeigten, daß es unter der Voraussetzung 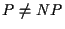$P\neq NP$ keinen polynomiellen Approximationsalgorithmus mit Gütegarantie kleiner als 14/13 geben kann. Für eine besondere Klasse von Problemen liegt diese Schranke sogar bei 2, was sich mit der Gütegarantie des besten bekannten Approximationsalgorithmus deckt. Dies löste ein offenes Problem von Ravi, Rosencrantz und Tayi. Andererseits gelang es uns für eine andere Problemklasse, diesen besten bekannten Approximationsfaktor zu verbessern, indem wir einen polynomiellen Approximationsalgorithmus mit Gütegarantie 3/2 entwickelten.

  

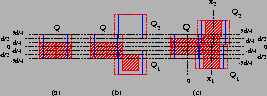
Abbildung 1.14: Konstruktion des 2/3-Approximationsalgorithmus