Abbildung: Ausschnitt aus einem wöchentlichen Flugplan
Die Deutsche Lufthansa bietet wöchentlich knapp 10.000 Flüge an, die jeweils von einem der rund 250 Flugzeuge der Flotte bedient werden müssen. Jeder Flug wird von einer vier- bis achtköpfigen Crew begleitet, die aus dem 11.000 Menschen zählenden Flugpersonal des Unternehmens zusammengestellt wird. Die Erstellung möglichst kostengünstiger Flugpläne ist das Ziel dieses Projektes, welches von uns in Kooperation mit der Lufthansa Systems GmbH, der Gesamthochschule/Universität Paderborn und der Humboldt-Universität zu Berlin bearbeitet wird. Unser Hauptarbeitsgebiet ist dabei das Fleet Assignment, d.h. die optimale Zuordnung von Flugzeugtypen zu gegebenen Flugstrecken.
Beim Entwurf eines neuen Flugplans bestimmt die Gesellschaft zunächst, welche Verbindung zu welchem Zeitpunkt angeboten werden soll. Die Überprüfung, ob ein solcher Flugplan mit dem vorhandenen Material und den Beschäftigten realisierbar ist, erfordert einen hohen Einsatz von Erfahrung und Rechnerpotential. Dabei sind Wartungsintervalle und viele andere Restriktionen zu beachten. Bei der Kosten-Nutzen-Berechnung spielt die Analyse von Zubringerflügen eine herausragende Rolle. Es ist zu klären, wieviele Menschen, die beispielsweise die gewinnbringende Route von Köln über Frankfurt nach New York gebucht haben, überhaupt zum richtigen Zeitpunkt in Frankfurt sein können und wieviele Passagiere, die anschließend weiter nach Seattle, Miami oder San Francisco fliegen möchten, ebenfalls mitgenommen werden können. Darüber hinaus ist zu klären, ob der erstellte Flugplan eine effiziente Personaleinsatzplanung ermöglicht (Ruhepausen, Übernachtungskosten etc.). Der ungeheure Umfang des Problems ergibt sich daraus, daß jede Woche eine halbe Million solcher Reiserouten angeboten wird.
Beim Flugplandesign wird meist so vorgegangen, daß ein historisch gewachsener Flugplan an wenigen Stellen leicht modifiziert wird. So kann sich die Überprüfung der Realisierbarkeit sowie die Kostenbewertung an früheren Ergebnissen orientieren. Aufgrund des sich zunehmend verschärfenden Wettbewerbs müssen heute regelmäßig völlig neue Flugpläne entworfen werden. Rechner, wegen der Datenfülle insbesondere Parallelrechner, helfen dem Flugplandesigner dabei, ein konkurrenzfähiges Angebot der Gesellschaft für den Kunden zu erstellen.
Nachdem geklärt wurde, zu welchem Zeitpunkt eine Flugverbindung (,,Leg``) angeboten wird, wird als nächstes festgelegt, welcher Flugzeugtyp (,,Equipment``), beziehungsweise welches konkrete Flugzeug (,,Tail``) einen Flug bedienen soll. Die Flugzeuge unterscheiden sich in der Kapazität, also der maximalen Anzahl der Passagiere, der maximalen Reichweite, sowie in den Kosten, die pro geflogenem Kilometer und befördertem Passagier verursacht werden. Durch das Fleet Assignment wird festgelegt, welcher Flugzeugtyp für die Gültigkeitsdauer des Flugplans jede Woche für eine bestimmte Flugverbindung verwendet wird. Die Kosten, die beim Fleet Assignment minimiert werden, sind vor allem Energiekosten. Diese liegen schon bei einem wöchentlichen Flugplan bei mehreren Millionen Mark.
Eine graphentheoretische Modellierung des Fleet-Assignment-Problems wird durch
einen gerichteten Graphen D=(V,A) gegeben, wobei die Knotenmenge V
der Menge der einzelnen Direktflüge entspricht. Zwei Knoten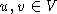 
werden durch eine gerichtete Kante von u nach v
verbunden, wenn es möglich ist, erst den Flug u und
anschließend den Flug v mit demselben Flugzeug zu bedienen. Ein
Fleet Assignment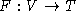 
weist jedem Flug 
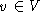einen
Flugzeugtyp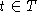 
zu.
Zur Lösung von Fleet-Assignment-Problemen kleinerer Fluggesellschaften wird in der Literatur häufig ganzzahlige lineare Optimierung vorgeschlagen. Die Komplexität des zugrundeliegenden Mehrgüterflußproblems (die Flugzeugtypen werden als Güter aufgefaßt, die durch den Graphen D transportiert werden müssen) läßt dieses Vorgehen jedoch bei größeren Problemen nicht zu. Bei drei oder mehr verschiedenen Flugzeugtypen ist das Problem NP-schwer.
Eine Zuweisung kann aber gefunden werden, wenn die betrachtete Flottenmenge sukzessive in jeweils zwei Untermengen unterteilt wird, und ein Fluß durch den Graphen festlegt, welcher Flug von einer der beiden Mengen bedient wird. Bestehen die einzelnen Untermengen im Verlauf dieser Heuristik nur noch aus je einem Flugzeugtyp, hat man eine Lösung des Fleet-Assignment-Problems gefunden. Unsere Untersuchungen ergaben, daß eine solche Heuristik auf einer mittleren Workstation etwa 30 Minuten benötigt, um ein Fleet Assignment zu bestimmen. Ein gegebenes Assignment kann anschließend mit Austauschheuristiken oder Simulated Annealing mit einigen Stunden Rechenzeit noch nachgebessert werden.
Hierbei betrachtet man nun den Flugplangraphen G=(V,A)
mit Flughafenmenge V und Teilflugmenge
A. Die Nachbarschaft eines Flugplanes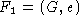 
(mit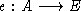 
, E Equipmentmenge) ist durch alle Flugpläne F
gegeben, die sich auf genau einem gerichteten Kreis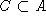 
(mit
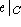konstant in F bzw. G) in dem darauf eingesetzten Equipment
unterscheiden. Die zu minimierende Zielfunktion wird dabei aus der
Differenz der Kosten und Erlöse pro Passagier
gebildet. Zum Auffinden eines Nachbarn, also zum Finden eines
solchen ,,Equipment-Kreises`` in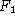 
, verwenden wir eine
Depth-First-Search-Strategie.
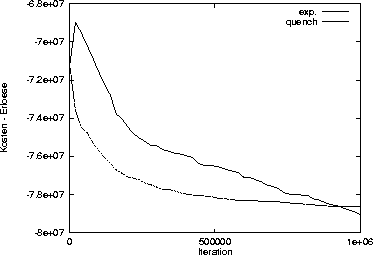
Abbildung: Die Zielfunktion mit einem exponentiellen Cooling Schedule
und mit Quenching
Sowohl das Simulated-Annealing-Verfahren als auch unsere auf Flußalgorithmen basierende Heuristik sind leicht parallelisierbar. Simulated Annealing liegt bereits in einer parallelen Version vor. Realisiert wurde dies mit dem Message-Passing-Interface, was größtmögliche Portabilität gewährleistet. Sowohl die sequentiellen Algorithmen als auch das parallele Simulated Annealing liefern bereits gute Resultate. Mit Ergebnissen der weiteren Parallelisierungen rechnen wir planungsgemäß Ende 1996/Anfang 1997.
Die bisher erzielten Ergebnisse zeigen eine Gewinnsteigerung um bis zu 11 Prozent gegenüber der vorhandenen Startlösung, die einem historischen Flugplan der Lufthansa entspricht. Gleichzeitig konnten die Größen der benötigten Teilflotten reduziert werden. Verbesserungen erwarten wir vor allem in der Laufzeit, die derzeit einige Stunden beträgt.
Abbildung: Ein Ausschnitt aus dem von uns berechneten wöchentlichen Einsatzplan
Ist das Fleet Assignment festgelegt, so wird der wöchentliche
Einsatzplan der einzelnen Flugzeuge bestimmt. Hierbei müssen wieder neue
Restriktionen, insbesondere Wartungsintervalle, beachtet werden. Für
jeden Flugzeugtyp 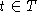ist eine Zahl 
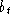gegeben, die angibt,
wieviele einzelne Flugzeuge des Typs t vorhanden sind.
Für ein Fleet Assignment seien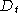 
die durch das Assignment
induzierten Subgraphen von D mit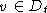 
, wenn F(v)=t ist. Für
jeden induzierten Subgraphen ist die minimale Anzahl von Ketten, die
ihn überdecken, gleich der Anzahl der zu verwendenden Flugzeuge.
Diese Zahl läßt sich mit Matchingalgorithmen in polynomieller Zeit
berechnen. Ist sie kleiner als 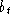für alle 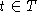, so ist das
Fleet Assignment unter dem Gesichtspunkt der rotationellen Verknüpfung
zulässig. Eine überdeckende Kette entspricht dann dem Wochenplan
eines Flugzeugs. Diese Berechnungsphase braucht pro Flugzeugtyp wenige
Sekunden Rechenzeit auf einer mittleren Workstation.
Bereits während des Aufbaus eines Fleet Assignments werden die Erträge überprüft, die sich durch eine Zuweisung erwarten lassen. Hierbei gilt es vor allem, die Passagierzusammensetzung auf Flügen, die von verschiedenen Reiserouten benutzt werden, zu kontrollieren. Eine Reiseroute wird im graphentheoretischen Modell als Hyperkante aufgefaßt, die aus mehreren Knoten, den zugehörigen Flügen, besteht. Diese Kanten werden durch den Ertrag, den ein Passagier auf dieser Route einbringt, bewertet. Auf den Knoten gibt die Kapazität des Flugzeugtyps die Zahl der Passagiere an, die auf diesem Flug transportiert werden können.
Auf den Reiserouten werden jetzt verschiedene Güter, d.h. die Passagiere, möglichst günstig durch das Netzwerk transportiert, so daß für jedes Gut in jedem Knoten die Flußerhaltung gewährleistet bleibt. Die Lösung dieses Mehrgüterflußproblems bestimmt den Wert des Fleet Assignments. Aufgrund der Datenmenge ist vor allem in dieser Berechnungsphase der Einsatz von Höchstleistungsrechnern unerläßlich, auf denen dann parallele Flußtechniken zum Einsatz gebracht werden.