Startseite    
MathematikPoolNRW Projekt Hintergründe Kontakt


Das konjugierte Gradientenverfahren (n=2)


Gradient, Hessematrix

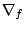
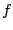
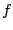
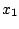
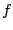
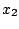
Der Gradient $\nabla_f$ der Funktion $f$ ist das Tupel, das sich aus der Ableitung von $f$ nach $x_1$ und der Ableitung von $f$ nach $x_2$ zusammensetzt, d.h. es ist
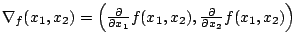
$\nabla_f(x_1,x_2) = \left(\frac{ \partial}{\partial x_1} f(x_1,x_2), \frac{ \partial}{\partial x_2} f(x_1,x_2) \right)$.
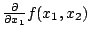
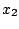
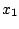
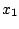
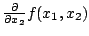
Die partielle Ableitung $\frac{ \partial}{\partial x_1} f(x_1,x_2)$ berechnet man, indem man sich $x_2$ als feste Zahl und $x_1$ als Veränderliche vorstellt und dann wie aus der Differentialrechnung mit einer Veränderlichen gewohnt nach $x_1$ ableitet. Die partielle Ableitung $\frac{ \partial}{\partial x_2} f(x_1,x_2)$ behandelt man analog.

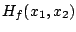
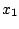
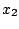
Die Hessematrix $H_f(x_1,x_2)$ erhält man, indem die beiden Komponenten des Gradienten nochmals jeweils nach $x_1$ und $x_2$ abgeleitet werden, d.h. es ist
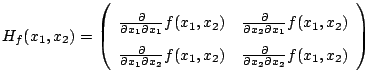
$ H_f(x_1,x_2) = \left( \begin{array}{ccc} \frac{ \partial}{\partial x_1 \par... ...\frac{ \partial}{\partial x_2 \partial x_2} f(x_1,x_2) \end{array} \right) $.

 


Beispiel:
Für die Funktion

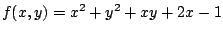         $f(x,y)=x^2+y^2+xy+2x-1$

ist der Gradient
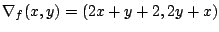         $\nabla_f(x,y)=(2x+y+2, 2y+x)$
und die Hessematrix
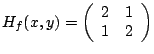         $ H_f(x,y) = \left( \begin{array}{cc} 2 & 1 \cr 1 &2 \end{array} \right) $.
.
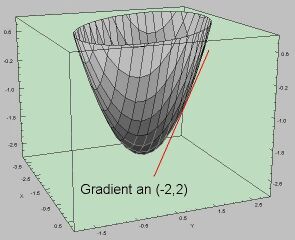
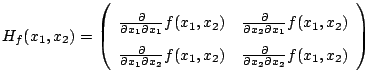