| Differenzengleichungen | Sparen mit Verzinsung | Exponentielles Wachstum | Logistisches Wachstum | Fixpunkte | Stabilität | Zyklen | Chaos |
Mit Differenzengleichung lassen sich Änderungen von Zustandsgrößen
mit der Zeit beschreiben. Im Unterschied zu Differentialgleichungen wird
dabei nicht davon ausgegangen, dass diese Veränderungen kontinuierlich
erfolgen, sondern es werden nur die Übergänge von Zeitpunkt t zum Zeitpunkt
![]() betrachtet.
betrachtet.
![]()
Im folgendem wird aus Gründen der Einfachheit
![]() gleich 1 gesetzt.
Eine Einheit vernachlässigen wir hierbei.
Tritt X(t) auf der rechten Seite der Gleichung nicht als Argument einer Funktion
und nur mit der Potenz 1 auf, dann ist die Differenzengleichung linear.
Alle anderen Differenzengleichungen heißen
nichtlinear.
gleich 1 gesetzt.
Eine Einheit vernachlässigen wir hierbei.
Tritt X(t) auf der rechten Seite der Gleichung nicht als Argument einer Funktion
und nur mit der Potenz 1 auf, dann ist die Differenzengleichung linear.
Alle anderen Differenzengleichungen heißen
nichtlinear.
Als Beispiel kann man einen Sparer betrachten, der zum Ersten eines Monats
eine Sparrate auf sein Sparkonto einzahlt.
Sein Guthaben wird ihm verzinst.
Um die Rechnung möglichst einfach zu halten, nehmen wir an, dass diese
Verzinsung ebenfalls monatlich, allerdings zum Monatsende, erfolgt.
Damit ist auch seine Spargeldeinzahlung einen gesamten Monat auf dem Konto.
Den Zinssatz pro Monat bezeichnen wir mit p und berechnen damit den
Aufzinsungsfaktor q.
Der Aufzinsungsfaktor entspricht einfach dem Faktor mit dem man das Kapital
multiplizieren muss, um das des nächsten Zeitpunktes zu bestimmen.
Ist also p in Prozent gegeben, dann gilt q=1+p/100.
Weiterhin gehen wir davon aus, dass er eine gleichbleibende Rate r
einzahlt.
Nehmen wir an, dass der Sparer mit einem Kapital
![]() startet.
Betrachten wir nun, wie sich das Kapital verändert
startet.
Betrachten wir nun, wie sich das Kapital verändert
![]()
![]()
![]()
![]()
![]()
Wegen ![]() folgt
folgt
![]()
Betrachten wir einen anderen Vorgang, die exponentielle Wachstumsgleichung.
Die logistische Abbildung gleicht formal der logistischen Wachstumsgleichung. Wenn man die kontinuierliche Wachstumsgleichung mit dem Eulerverfahren diskretisiert, dann ergibt sich als Ergebnis die log. Abbildung. Sie lässt sich aber im Gegensatz zu der anderen Gleichung nicht mehr analytisch lösen.
![]()
Dafür kann sie in Abhängigkeit von r noch unterschiedlicheres Verhalten bis hin zum Chaos zeigen. Um das Verhalten der log. Abbildung näher zu untersuchen geht man ähnlich vor, wie bei Differentialgleichungen. Man kann zu einem die stationären Lösungen bestimmen. Zum anderen könnte man die Gleichung vom Computer bis zu einem Zeitpunkt ausrechnen lassen.
Stationäre Lösungen von Differenzengleichungen sind ähnlich wie bei Differentialgleichungen die Punkte, bei denen keine Veränderungen mehr erfolgen. Keine Veränderung bei Differenzengleichungen heißt, dass X(t+1)=X(t) gilt. Mit dieser Bedingung lassen sich die stationären Lösungen, die bei Differenzengleichungen auch Fixpunkte genannt werden, bestimmen. Als erstes Beispiel betrachten wir die exp. Gleichung:
![]()
Bedingung: ![]() .
.
Die Bedingung ist offensichtlich erfüllt,
wenn: a)
![]() oder b) r=1 ist. Beide Lösungen sind offensichtlich.
Wenn kein X vorhanden ist, dann kann es sich auch nicht verändern.
Oder wenn die Wachstumsrate eins ist, ist ebenfalls jede Veränderung ausgeschlossen.
Die exponentielle Wachstumsgleichung ist ein lineares System.
Hier kann nur ein Fixpunkt vorliegen (außer bei r=1), der entweder stabil oder instabil ist.
Anders sieht das bei nichtlinearen Differenzengleichungen aus.
oder b) r=1 ist. Beide Lösungen sind offensichtlich.
Wenn kein X vorhanden ist, dann kann es sich auch nicht verändern.
Oder wenn die Wachstumsrate eins ist, ist ebenfalls jede Veränderung ausgeschlossen.
Die exponentielle Wachstumsgleichung ist ein lineares System.
Hier kann nur ein Fixpunkt vorliegen (außer bei r=1), der entweder stabil oder instabil ist.
Anders sieht das bei nichtlinearen Differenzengleichungen aus.
![]()
hat zwei Gleichgewichtspunkte:
Den Punkt
![]() und den Punkt
und den Punkt
![]() .
.
Um die Stabilität zu untersuchen, geht man ähnlich wie bei den Differentialgleichungen vor. Wir haben die Ausgangsgleichung:
![]()
mit dem Fixpunkt
![]() .
Zuerst führt man wieder einen Störungsterm
.
Zuerst führt man wieder einen Störungsterm
![]() ein.
Gilt nun,
dass
ein.
Gilt nun,
dass ![]() gegen Null strebt, wenn t immer größer wird,
dann ist
gegen Null strebt, wenn t immer größer wird,
dann ist ![]() stabil.
Zunächst einmal formen wir den Ausdruck oben ein wenig um.
stabil.
Zunächst einmal formen wir den Ausdruck oben ein wenig um.
![]() . Damit haben wir dasselbe für
. Damit haben wir dasselbe für ![]() .
Wir setzen beide Ausdrücke in die Differenzengleichung von oben ein
.
Wir setzen beide Ausdrücke in die Differenzengleichung von oben ein
![]()
und führen wieder die Taylorreihenentwicklung durch.
![]()
Da ![]() (Fixpunkt!) bekommt man:
(Fixpunkt!) bekommt man:
![]()
Damit heben wir die exp. Wachstumsgleichung und können folgendes Verhalten erkennen:
Als Beispiel wird die Stabilität der beiden Fixpunkte der log. Wachstumsgleichung
bestimmt.
Man berechnet zunächst die Ableitung von f(X(t)) nach X(t).
![]()
Nun trifft man die folgende Fallunterscheidung:
1) ![]()
Damit: ![]() . Damit ist dieser Gleichgewichtspunkt instabil,
sobald der Wachstumsparameter vom Betrage her eins überschreitet.
. Damit ist dieser Gleichgewichtspunkt instabil,
sobald der Wachstumsparameter vom Betrage her eins überschreitet.
2) ![]()
Es ist
![]()
Gilt r<0, dann ist der zweite Fixpunkt instabil.
Stabil ist er für den Bereich 1<r<3. Dabei zeigt er folgendes
Verhalten. Bis zum Wert 2 bewegt sich X(t) monoton auf den Gleichgewichtspunkt zu.
Bei einem Wert größer als 2 hingegen fängt das System an zu schwingen.
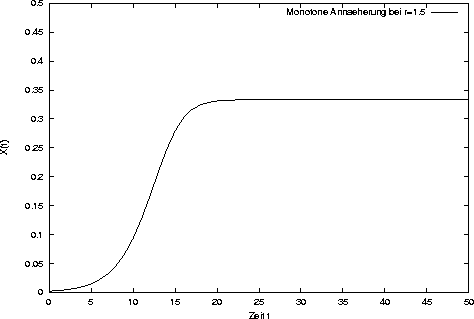
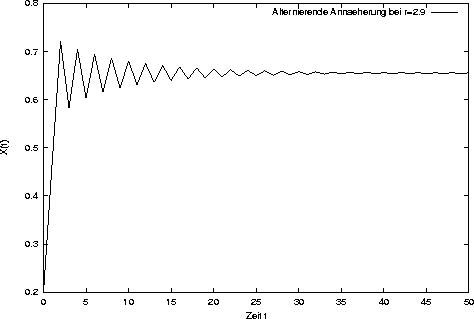
Zyklen in einem System treten auf, wenn periodische Schwingungen vorliegen. Das heißt nach einer bestimmten Zeitspanne wird der Punkt genau wieder erreicht und das System beginnt von vorne. Zyklen werden unterschieden nach ihrer Periode, d.h. nach der Zeit, die sie brauchen, um wieder in den Ausgangspunkt zurückzukehren. Fixpunkte sind gewissermaßen Zyklen mit der Periode eins. Die formale Definition eines Zyklus mit der Periode k lautet:
![]()
Es wurde bereits bei der logistischen Abbildung erwähnt, dass der zweite Fixpunkt instabil wird, sobald der Wachstumsparameter den Wert 3 überschreitet. Man kann jetzt zeigen, dass der Fixpunkt gewissermaßen von einem Zyklus mit der Periode 2 abgelöst wird.
Die Vorgehensweise ist wie bei einem Fixpunkt. Man hat die Forderung:1:X(t+2)=X(t), und 2:X(t+1)!=X(t). Damit muss man alle Punkte berechnen, die die erste Gleichung erfüllen. Danach setzt man sie in die zweite ein und nimmt schließlich alle Punkte, die diese nicht erfüllen. Die Rechnung führt hier auf ein Polynom dritter Ordnung und wird hier nicht durchgeführt. Auch die Stabilität (lokal) von Zyklen kann man wieder mit der Taylorreihe und dem Störungsterm zeigen. Die Ausbildung eines periodischen Verhaltens bei der log. Abbildung ist hier ein erster Schritt zum chaotischen Verhalten der Gleichung.
Mit dem Begriff Chaos wird zumeist folgendes Verhalten umschrieben.
Wenn man bei der log. Abbildung dem Wert von r weiter nach oben verschiebt,
dann kann man folgendes erreichen.
Sobald der Wert von r die 3 überschreitet, beginnt ein periodisches Verhalten.
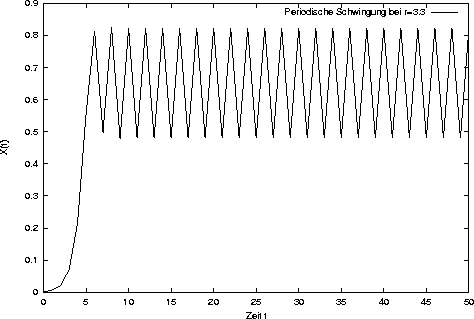
Zunächst noch mit der Periode 2, d.h.
nach zwei Zeitschritten ist das System wieder im Ausgangspunkt.
Wie man erkennt, werden damit quasi zwei Eckpunkte immer wiederholt.
Vergrößert man den Wert von r weiter, beginnen sich die Perioden zu verdoppeln.
Bei einem Wert größer als 3.4495 liegt bereits Periode 4 vor.
Periode 8 tritt bei 3.5441 auf, Periode 16 bei 3.5644, danach, bis die 3.57 erreicht wird,
verdoppelt sich die Periode immer weiter, wobei die Abstände immer kürzer werden.
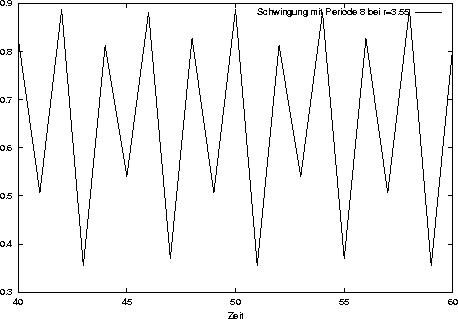
Feigenbaum konnte zeigen, dass die Längen zweier aufeinander folgender Intervalle miteinander
in Beziehung stehen.
![]()
Die Konstante wird nach ihm Feigenbaum-Konstante genannt und gilt für alle Intervalle bei
Periodenverdoppelung.
Bei einem Wert von 3.57 schließlich kippt das System ins Chaos. Es tritt erst einmal
kein periodisches Verhalten mehr auf.
In der folgendem Abbildung wurden die Werte von X(t) für zwei unterschiedliche Startwerte
über 50 Zeitschritte hinweg aufgetragen.
Man erkennt, dass keine regelmäßigen Schwingungen mehr auftreten. Zudem verhalten sich
die beiden Kurven sehr unterschiedlich, obwohl die Startwerte nur um 0.001
auseinander liegen.
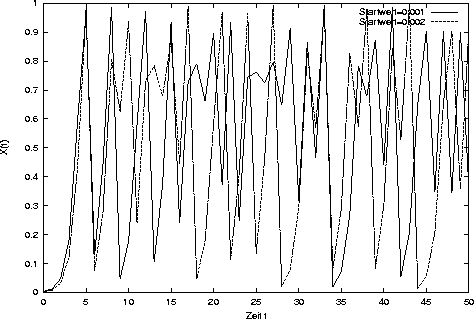
Ein interessantes Phänomen ist, dass sich für größere Werte von r für
kurze Abschnitte Fenster mit periodischen Verhalten ausbilden.
In der folgenden Abbildung wurden die stationären Punkte von X(t)
gegen den Wachstumsparameter r aufgetragen. Periodenverdoppelungen
erkennt man an den Gabelungen, die auch Bifurkationen genannt werden.
Die Lücken in der Abbildung sind die Fenster, in denen wieder periodisches
Verhalten auftritt.
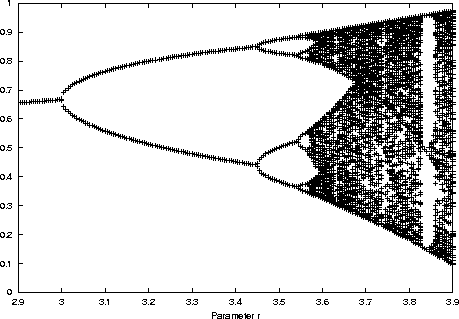
| Differenzengleichungen | Sparen mit Verzinsung | Exponentielles Wachstum | Logistisches Wachstum | Fixpunkte | Stabilität | Zyklen | Chaos |