| Differentialgleichungen | Exponentielles Wachstum | Logistisches Wachstum | Systeme | Räuber-Beute-Systeme | Gleichgewichtspunkte | Stabilität |
Eine Differentialgleichung beschreibt die Änderung einer Zustandsgröße
z.B. in Abhängigkeit der Zeit. Die Änderung der Zustandsgröße wird durch die Ableitung beschrieben.
Es gibt mehrere Formen von Differentialgleichungen. Einige
davon sollen kurz beschrieben werden.
Die untenstehende DGL ist ein Beispiel für eine explizite DGL 1.Ordnung.
Explizit heißt, dass die Ableitung ![]() isoliert werden kann
und alleine auf einer Seite der Gleichung steht.
Der Ausdruck 1.Ordnung bedeutet, dass nur die erste Ableitung
in die Gleichung eingeht.
isoliert werden kann
und alleine auf einer Seite der Gleichung steht.
Der Ausdruck 1.Ordnung bedeutet, dass nur die erste Ableitung
in die Gleichung eingeht.
![]()
Die folgende Gleichung ist eine DGL 2.Ordnung.
![]()
Die folgende DGL ist eine explizite, lineare DGL 1.Ordnung. Linear heißt, dass die Zustandsgröße X(t) linear ist.
![]()
Die folgenden Gleichung ist damit nicht mehr linear.
![]()
Die Lösung von Differentialgleichungen erfolgt über Integration, wenn dies durchführbar ist. Häufig erfordern die Lösungsvorgänge umfangreiche Umformungen der Ausgangsgleichungen. In den meisten Simulationsprogrammen werden DGLs durch numerische Approximationsverfahren gelöst (Euler-Cauchy oder Runge-Kutta). Diese Näherungslösungen führen gelegentlich zu größeren Ungenauigkeiten oder sogar zu völlig falschen Resultaten.
Man spricht von einem Wachstum, wenn ![]() , bei
, bei ![]() für
alle
für
alle ![]() . Eine
der einfachsten Formen von Wachstum ist das exponentielle Wachstum.
Hier wird angenommen, dass die Änderung proportional zu der vorhandenen
Masse (oder Zahl) ist.
Wenn man z.B. eine Bakterienpopulation betrachtet, kann man im ersten
Ansatz davon ausgehen, dass zwei Vorgänge das Wachstum bestimmen:
Die Bakterien vermehren sich und sie sterben ab.
Die Vermehrung hängt davon ab,
wie viele Bakterien vorher vorhanden waren, ebenso die Abnahme.
Wir können nun eine Sterbe- und Geburtenrate (Teilungsrate usw.)
einführen und die beiden Vorgänge erst einmal in der Wachstumsrate r zusammen
führen.
. Eine
der einfachsten Formen von Wachstum ist das exponentielle Wachstum.
Hier wird angenommen, dass die Änderung proportional zu der vorhandenen
Masse (oder Zahl) ist.
Wenn man z.B. eine Bakterienpopulation betrachtet, kann man im ersten
Ansatz davon ausgehen, dass zwei Vorgänge das Wachstum bestimmen:
Die Bakterien vermehren sich und sie sterben ab.
Die Vermehrung hängt davon ab,
wie viele Bakterien vorher vorhanden waren, ebenso die Abnahme.
Wir können nun eine Sterbe- und Geburtenrate (Teilungsrate usw.)
einführen und die beiden Vorgänge erst einmal in der Wachstumsrate r zusammen
führen.
![]()
Zum Lösen dieser Gleichung muss beachtet werden, dass die Ableitung
des natürlichen Logarithmus (ln(x)) gegeben ist durch ![]() , zusätzlich muss noch
die Kettenregel angewendet werden.
Wir bringen als erstes X(t) auf die linke Seite der Gleichung.
, zusätzlich muss noch
die Kettenregel angewendet werden.
Wir bringen als erstes X(t) auf die linke Seite der Gleichung.
![]()
Auf der linken Seite der Gleichung steht dann die Ableitung von ln(X(t).
(Wer Verständnisprobleme hat, kann es durch Differenzieren nachrechnen.)
![]()
Wir können jetzt beide Seiten über t integrieren, als Integrationsbereich wählen wir 0 bis s.
![]()
![]()
![]()
![]()
Delogarithmieren beider Seite der Gleichung führt zu
![]()
![]()
Damit hat man die Lösung der exponentiellen Wachstumsgleichung bestimmt. Der Ausdruck X(0) ist der Startwert für die Zustandsgröße. Wenn man das Wachstum einer Population betrachtet, ist es die Ausgangsgröße der Population. Wenn r größer Null ist, dann wächst die Population exponentiell. Ist r hingegen kleiner Null, dann liegt ein exponentieller Zerfall vor; die Population stirbt aus.
Das logistische Wachstum berücksichtigt im Gegensatz zum exponentiellen Wachstum die Tatsache, dass kein Wachstum unbegrenzt fortsetzbar ist. Vielmehr wird irgendwann eine Kapazitätsgrenze K erreicht werden, die nicht überschritten werden kann. Wenn man das Wachstum von Bakterien in einer Nährstofflösung betrachtet, dann reichen die Nährstoffe nur für eine bestimmte Zahl von Bakterien aus. Ist diese Schwelle erreicht, nimmt die Population nicht weiter zu. In der Natur ist deshalb häufig ein S-förmiger Verlauf der Wachstumskurve zu beobachten. Die Differentialgleichung, die einen solchen Verlauf widerspiegelt, ist die logistische Wachstumsgleichung:
![]()
Man kann den Wachstumsparameter r und die Kapazitätsgrenze K zu einen
neuen Parameter ![]() zusammenfassen.
Diese Form der Gleichung findet sich auch häufig.
zusammenfassen.
Diese Form der Gleichung findet sich auch häufig.
![]()
Wenn man die logistische Wachstumsgleichung betrachtet, dann fällt folgendes auf:
Solange X(t) noch klein ist,
kann man das Produkt ![]() vernachlässigen,
da es nur noch kleiner ist (denn:
vernachlässigen,
da es nur noch kleiner ist (denn: ![]() !).
Daher verhält sich die Gleichung anfangs wie die Gleichung für das
exponentielle Wachstum und flacht erst später ab.
Die logistische Wachstumsgleichung ist lösbar. Prinzipiell verfährt man wie
bisher. Man bringt alle Terme mit X(t) auf die linke Seite der Gleichung.
!).
Daher verhält sich die Gleichung anfangs wie die Gleichung für das
exponentielle Wachstum und flacht erst später ab.
Die logistische Wachstumsgleichung ist lösbar. Prinzipiell verfährt man wie
bisher. Man bringt alle Terme mit X(t) auf die linke Seite der Gleichung.
![]()
![]()
Man kann jetzt nicht sofort integrieren, weil im Nenner X(t) im Produkt
vorkommt. Was man erreichen möchte ist, dass das Produkt aufgelöst wird
und ![]() ersetzt wird durch einen Ausdruck wie
ersetzt wird durch einen Ausdruck wie
![]() .
Dazu verwendet man die bekannte Partialbruchzerlegung.
Wir gehen hierzu wie folgt vor:
.
Dazu verwendet man die bekannte Partialbruchzerlegung.
Wir gehen hierzu wie folgt vor:
Es existieren Konstanten A und B, so dass gilt:
![]()
Man bringt jetzt die Brüche auf der rechten Seite der Gleichung auf einen gemeinsamen Nenner.
![]()
![]() soll gleich
soll gleich ![]() sein.
Die Nenner sind gleich, also muss man den Zähler anpassen.
Man führt jetzt einen
Koeffizientenvergleich durch.
Das bedeutet nichts anderes, als dass man die Potenzen von X(t)
auf beiden Seiten der Gleichung vergleicht und
die Parameter A und B so anpasst, dass die Terme für jede Potenz übereinstimmen.
sein.
Die Nenner sind gleich, also muss man den Zähler anpassen.
Man führt jetzt einen
Koeffizientenvergleich durch.
Das bedeutet nichts anderes, als dass man die Potenzen von X(t)
auf beiden Seiten der Gleichung vergleicht und
die Parameter A und B so anpasst, dass die Terme für jede Potenz übereinstimmen.
Zuerst beginnt man mit den Konstanten:
Links steht AK, rechts 1. Man fordert Gleichheit: AK=1 und damit ![]() .
Damit ist der Parameter A bereits festgelegt.
.
Damit ist der Parameter A bereits festgelegt.
Danach geht man zu X(t) über.
Auf der linken Seite der Gleichung steht vor X(t) die Variablen -A+B.
Auf der rechten Seite kommt kein Ausdruck mit X(t) vor; damit ist der Wert 0.
Somit ergibt sich:
-A+B=0 und A=B. Damit hat man die beiden Ausdrücke für A und B bestimmt
und kann sie in die Gleichung (*) einsetzten.
Es ergibt sich der Ausdruck:
![]()
![]()
![]()
Jetzt kann man integrieren:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
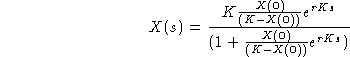
Man kann diese Gleichung noch weiter umformen, um die Auswertung zu erleichtern.
Im Zähler und im Nenner kommt der Ausdruck ![]() vor, der zuerst eliminiert
wird.
(Anmerkung
vor, der zuerst eliminiert
wird.
(Anmerkung ![]() kann auch geschrieben werden als:
kann auch geschrieben werden als: ![]() )
)
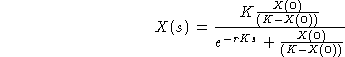
Störend ist jetzt noch, dass auch der Bruch ![]() sowohl im Zähler als auch im Nenner vorkommt.
sowohl im Zähler als auch im Nenner vorkommt.
![]()
Wenn s größer wird, geht ![]() gegen Null.
Das System strebt damit gegen die Kapazitätsgrenze K.
gegen Null.
Das System strebt damit gegen die Kapazitätsgrenze K.
Bisher wurde nur eine einzige isolierte Größe betrachtet. In der Realität werden Vorgänge nicht isoliert ablaufen können, sondern vielmehr durch andere Größen beeinflusst werden. Es gibt viele Definitionen des Begriffes System. Im Wesentlichen enthält ein System die Elemente und deren Verhalten mitsamt den Wechselwirkungen untereinander. Hierbei unterscheidet man die folgenden:
Wenn sich zwei (oder mehr) Größen gegenseitig beeinflussen, dann liegt eine Wechselwirkung vor. Die Auswirkung der Beziehung kann für die einzelnen Seiten Nutzen oder Schaden bringen und damit positiv oder negativ sein.
Wir betrachten im Folgenden je eine Population von Schneehasen und Luchsen. Weiterhin nehmen wir folgende Vorraussetzungen an:
![]()
![]()
![]()
![]()
Das Modell stammt von Lotka (1910; 1925) und wurde benutzt um den Zusammenhang von Hasen und Luchsen in einem Gebiet in Kanada zu beschreiben. (Eine Pelzkompanie war sehr interessiert an diesem Thema und lieferte Daten) Diese Gleichungen sind nicht explizit lösbar. Man kann sie mit Hilfe numerischer Approximation (Runge-Kutta o.ä.) darstellen. Oder man kann generell untersuchen, wie sich das System in Abhängigkeit von den Parametern b, m, r und den Startwerten für die Populationen verhält. Im folgenden Abschnitt soll die grundsätzliche Vorgehensweise erläutert werden.
Gleichgewichtspunkte eines Systems sind die Nullstellen der Differentialgleichungen, mit denen das System beschrieben wurde. Damit sind sie die Stellen, bei denen keine sichtbaren Änderungen mehr erfolgen. Alle Änderungen laufen zwar nach wie vor ab, gleichen sich aber gegenseitig aus. Wenn man nur eine einzige Population betrachten würde, wäre das dynamische Gleichgewicht die Stelle, an der sich die Geburten und die Sterbefälle vollkommen ausgleichen. Obwohl nachwievor Individuen sterben und geboren werden, ist auf der Ebene der Gesamtpopulation keine Änderung mehr erkennbar. Gleichgewichte dieser Art werden auch als Fließgleichgewichte bezeichnet. Betrachten wir als erstes Beispiel das logistische Wachstum
![]()
so sind die Gleichgewichtspunkte: ![]() und
und ![]() . Oder anders:
Wenn keine Population da ist, dann kann sie klarerweise auch nicht wachsen.
Gleiches gilt für die Kapazitätsgrenze.
. Oder anders:
Wenn keine Population da ist, dann kann sie klarerweise auch nicht wachsen.
Gleiches gilt für die Kapazitätsgrenze.
Für das Räuber-Beute-System aus dem obigen Abschnitt muss nun folgendes
gelten:
![]()
![]()
und das gleichzeitig.
Fangen wir mit der ersten Gleichung für die Luchse an.
![]()
Also entweder F(t)=0 oder (-m +rH(t))=0. Der zweite Ausdruck ist gleichbedeutend
mit ![]() .
Wir müssen dabei jetzt noch zusätzlich beachten, dass die zweite Gleichung für die Hasenpopulation auch Null sein muss.
.
Wir müssen dabei jetzt noch zusätzlich beachten, dass die zweite Gleichung für die Hasenpopulation auch Null sein muss.
![]()
Wir nehmen nacheinander die Gleichgewichtspunkte der ersten Gleichung und setzen
sie in die zweite ein.
Der erste Punkt ![]() führt zu der Forderung:
führt zu der Forderung:
![]()
Der zweite Punkt ![]() führt zu:
führt zu:
![]()
Also ![]() . Damit haben wir zwei mögliche Kombinationen von Gleichgewichtspunkten:
. Damit haben wir zwei mögliche Kombinationen von Gleichgewichtspunkten:
![]() oder
oder ![]() .
.
An beiden Punkten kommt das System quasi zu einem Halt, wenn es sie erreicht.
Die Frage ist jetzt, ob es diese Gleichgewichtspunkte erreicht.
Eine andere Frage ist, was passiert, wenn das System im Gleichgewichtspunkt ist
und dann gestört wird und sich damit aus ihm entfernt.
Kehrt es zurück oder bewegt es sich von ihm fort?
Wir interessieren uns daher für die Stabilität von Gleichgewichtspunkten.
Stabilität heißt im Wesentlichen, dass das System sich auf diese
Gleichgewichtspunkte zu bewegt.
Man kann mehrere Arten von Stabilität unterscheiden.
Die Untersuchung auf globale Stabilität ist häufig umständlich. Die lokale kann leichter untersucht werden. Hierfür muss ein kleiner Exkurs eingeführt werden.
Wir beginnen mit dem eindimensionalen Fall einer DGL.
![]()
Gleichgewichtspunkte sind alle die Punkte ![]() mit
mit ![]() .
Wir suchen damit die Nullstellen von f.
Wir wollen nun wissen, wann
.
Wir suchen damit die Nullstellen von f.
Wir wollen nun wissen, wann ![]() lokal stabil ist,
also unter welchen Umständen
X(t) nach einer geringen Auslenkung wieder nach
lokal stabil ist,
also unter welchen Umständen
X(t) nach einer geringen Auslenkung wieder nach ![]() zurückkehrt.
Dazu führt man eine Taylorreihenentwicklung um die
Gleichgewichtsstelle
zurückkehrt.
Dazu führt man eine Taylorreihenentwicklung um die
Gleichgewichtsstelle ![]() durch.
Auch die Taylorreihe ist gewissermaßen eine numerische Approximation.
Man geht davon aus, dass sich das System (oder vielmehr die DGL) in der
Nähe des Gleichgewichtspunktes durch die Ableitungen von f nach X beschreiben
lässt.
durch.
Auch die Taylorreihe ist gewissermaßen eine numerische Approximation.
Man geht davon aus, dass sich das System (oder vielmehr die DGL) in der
Nähe des Gleichgewichtspunktes durch die Ableitungen von f nach X beschreiben
lässt.
![]()
Man vernachlässigt nun alle Glieder höherer Ordnung und macht
eine lineare Approximation.
Prinzipiell behaupten wir nichts anderes, als dass sich ![]() durch die Steigung von f im Gleichgewichtspunkt und den Betrag der Auslenkung
approximieren lässt
(Wenn man f(x) gegen X aufgetragen hätte, dann zöge man gewissermaßen eine Gerade mit der Steigung
durch die Steigung von f im Gleichgewichtspunkt und den Betrag der Auslenkung
approximieren lässt
(Wenn man f(x) gegen X aufgetragen hätte, dann zöge man gewissermaßen eine Gerade mit der Steigung ![]() durch den Gleichgewichtspunkt).
Das geht nur solange gut, wie man in der Nähe von
durch den Gleichgewichtspunkt).
Das geht nur solange gut, wie man in der Nähe von ![]() ist,
ansonsten gewinnen die quadratischen
und kubischen Terme an Gewicht und man kann sie nicht mehr vernachlässigen.
Daher kann man hiermit nur die lokale Stabilität untersuchen.
Wir betrachten also:
ist,
ansonsten gewinnen die quadratischen
und kubischen Terme an Gewicht und man kann sie nicht mehr vernachlässigen.
Daher kann man hiermit nur die lokale Stabilität untersuchen.
Wir betrachten also:
![]()
![]()
und wollen wissen, ob wir wieder in den Gleichgewichtspunkt ![]() zurückkehren. Zunächst setzen wir
zurückkehren. Zunächst setzen wir ![]() , weil die Gleichungen
damit übersichtlicher werden. Es gilt Z'(t)=X'(t) und damit
, weil die Gleichungen
damit übersichtlicher werden. Es gilt Z'(t)=X'(t) und damit
![]()
Wir haben damit eine lineare DGL 1. Ordnung und können integrieren (vergl. Abschnitt über exponentielles Wachstum).
![]()
Ist ![]() , dann liegt exponentielles Wachstum vor, das System kehrt nicht zurück und
der Gleichgewichtspunkt ist instabil.
Ist
, dann liegt exponentielles Wachstum vor, das System kehrt nicht zurück und
der Gleichgewichtspunkt ist instabil.
Ist ![]() , dann hat man einen exponentiellen Zerfall, das System kehrt nach der anfänglichen Störung
in den Gleichgewichtspunkt zurück. Der Punkt
, dann hat man einen exponentiellen Zerfall, das System kehrt nach der anfänglichen Störung
in den Gleichgewichtspunkt zurück. Der Punkt ![]() ist stabil.
Gilt
ist stabil.
Gilt ![]() , so lässt sich erst einmal nichts Näheres aussagen.
, so lässt sich erst einmal nichts Näheres aussagen.
Die Vorgehensweise nennt sich auch lineare Stabilitätsuntersuchung.
Ähnliches wie im eindimensionalen Fall, kann auch im höherdimensionalen
durchgeführt werden. Wenn man zwei gekoppelte Zustandsgrößen
(z.B. Luchse ( ![]() )und Hasen (
)und Hasen ( ![]() )) hat, dann muss man zuerst die
Nullstellen von
)) hat, dann muss man zuerst die
Nullstellen von ![]() und
und ![]() bestimmen. Das heißt, man sucht alle
bestimmen. Das heißt, man sucht alle ![]() mit
mit
![]() und
und ![]() .
Man kann die beiden Gleichungen auch zusammenfassen und als Vektorgleichung schreiben.
.
Man kann die beiden Gleichungen auch zusammenfassen und als Vektorgleichung schreiben.
![]()
Hat man die Nullstellen bestimmt,
dann kann man wieder die Taylorreihenentwicklung durchführen.
Man bestimmt also wieder die erste Ableitung von f nach X.
Dabei gibt es im Vergleich zum eindimensionalen Fall einen Unterschied:
Die Funktion f setzt sich aus zwei Funktionen zusammen,
und diese Funktionen ![]() und
und ![]() wiederum hängen von
jeweils zwei Größen ab.
Um die Gesamtableitung (mit Df(X) bezeichnet) zu bestimmen,
müssen die Funktionen jeweils nach
wiederum hängen von
jeweils zwei Größen ab.
Um die Gesamtableitung (mit Df(X) bezeichnet) zu bestimmen,
müssen die Funktionen jeweils nach
![]() und
und ![]() abgeleitet und in die folgende Reihenfolge gebracht werden.
abgeleitet und in die folgende Reihenfolge gebracht werden.
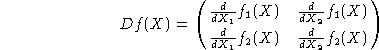
Der Ausdruck Df(X) wird daher auch Ableitungsmatrix von f(X) bezeichnet. Man kann die Gleichung formal wie oben umschreiben:
![]()
Diese Gleichung kann wieder ausintegriert werden, das erfordert aber eine umfangreichere Einführung. Genauer gesagt: Die Lösung ist wie im eindimensionalen Fall:
![]()
Probleme bereitet der Ausdruck ![]() , der unhandlich wird.
Das System wird jetzt normalerweise transformiert, damit man leichter rechnen kann.
Dies geschieht über die Eigenwerte und Eigenvektoren der Matrix
, der unhandlich wird.
Das System wird jetzt normalerweise transformiert, damit man leichter rechnen kann.
Dies geschieht über die Eigenwerte und Eigenvektoren der Matrix ![]() .
Eine Einführung in dieses Thema würde allerdings an dieser Stelle zu
aufwendig werden, so das hier nur die Ergebnisse angegeben
werden sollen.
Im Folgendem ist:
.
Eine Einführung in dieses Thema würde allerdings an dieser Stelle zu
aufwendig werden, so das hier nur die Ergebnisse angegeben
werden sollen.
Im Folgendem ist:
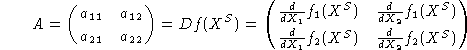
Gilt jetzt:
![]() und
und ![]() ,
dann ist der Gleichgewichtspunkt stabil und das System läuft
auf ihn zu.
Das kann entweder monoton geschehen oder mit Schwingungen.
,
dann ist der Gleichgewichtspunkt stabil und das System läuft
auf ihn zu.
Das kann entweder monoton geschehen oder mit Schwingungen.
Gilt:
![]() und
und ![]() dann ist der Gleichgewichtspunkt stabil und das System umkreist ihn.
Die Amplitude des Kreises oder der Schwingung hängt dabei von den
Anfangsbedingungen für X(t) ab.
dann ist der Gleichgewichtspunkt stabil und das System umkreist ihn.
Die Amplitude des Kreises oder der Schwingung hängt dabei von den
Anfangsbedingungen für X(t) ab.
Um das Vorgehen zu verdeutlichen, wird das Räuber-Beute-System als Beispiel
dargestellt.
![]()
Man leitet zunächst einmal ![]() nach F(t) ab. Dabei wird H(t) wie eine
Konstante behandelt.
nach F(t) ab. Dabei wird H(t) wie eine
Konstante behandelt.
![]()
Dann wird ![]() nach H(t) abgeleitet (in diesem Fall wird dann F(t) wie
eine Konstante behandelt).
nach H(t) abgeleitet (in diesem Fall wird dann F(t) wie
eine Konstante behandelt).
![]()
Schließlich wird beides noch für ![]() durchgeführt.
durchgeführt.
![]()
![]()
Wir erhalten damit die Systemmatrix:
![]()
In den Ausdruck setzt man nacheinander die beiden Gleichgewichtspunkte
ein.
1) ![]() .
.
![]()
Damit gilt ![]() und
und ![]() .
Da sowohl m als auch b größer als Null sind, ist der Nullpunkt nicht stabil.
.
Da sowohl m als auch b größer als Null sind, ist der Nullpunkt nicht stabil.
2) ![]()
![]()
Nun ist ![]() und
und ![]() .
Mit m, b ;SPMgt; 0 gilt, dass der zweite Gleichgewichtspunkt stabil ist.
Das System erreicht ihn allerdings nicht, sondern umkreist ihn in Bahnen,
deren Radius von den Anfangsbedingungen abhängen.
.
Mit m, b ;SPMgt; 0 gilt, dass der zweite Gleichgewichtspunkt stabil ist.
Das System erreicht ihn allerdings nicht, sondern umkreist ihn in Bahnen,
deren Radius von den Anfangsbedingungen abhängen.
![]()
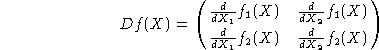
Setze:
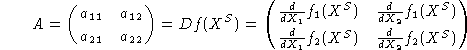
| Differentialgleichungen | Exponentielles Wachstum | Logistisches Wachstum | Systeme | Räuber-Beute-Systeme | Gleichgewichtspunkte | Stabilität |